Yaagyanika Gehlot¹, Bhairvi Sharma¹, P. Muthu¹, Hariharan Muthusamy¹ and S. Latha²

¹Department of Biomedical Engineering SRM Institute of Science and Technology, Kattankulathur, Chennai, Tamil Nadu, India.

²Department of Electronics and Communication Engineering SRM Institute of Science and Technology, Kattankulathur, Chennai, Tamil Nadu, India.

Corresponding Author E-mail: muthu.p@ktr.srmuniv.ac.in

DOI : https://dx.doi.org/10.13005/bpj/1526

Abstract

Silver nitrous aqueous solution is used to biosynthesize Silver nanoparticles (Ag-NPs) through a green and easy way using tuber powder extracts of Curcuma Longa (C. longa). The aim is to model an Artificial Neural Network (ANN) using seven existing algorithms in MATLAB for forecasting the size of the silver nanoparticle with volume of both C. longa extraction and AgNO3, time of stirring and temperature of reaction as input functions. Several techniques including Quasi-Newton, Conjugate Gradient and Levenberg-Maquardt are employed for training the designed ANN model, a feed-forward backpropagation network with different combinations of architecture and transfer functions. Each algorithm is fashioned to obtain the best performance by calculating the Regression (R), Mean Square Error (MSE), Mean Absolute Error (MAE) and Error Sum of Squares (SSE), thereby comparing the results and propounding the optimum algorithm technique for the discussed application in nanoengineering. Finally, based on the findings, the optimum network is proposed through the simulation results.

Keywords

Artificial Neural Network; Feed-forward Back Propagationl Learning Algorithms; Nanoengineering, Silver Nanoparticles

Download this article as: 

Copy the following to cite this article: Gehlot Y, Sharma B, Muthu P, Muthusamy H, Latha S. Biomedical Prediction of Radial Size of Powdered Element using Artificial Neural Network. Biomed Pharmacol J 2018;11(3).

Copy the following to cite this URL: Gehlot Y, Sharma B, Muthu P, Muthusamy H, Latha S. Biomedical Prediction of Radial Size of Powdered Element using Artificial Neural Network. Biomed Pharmacol J 2018;11(3). Available from: http://biomedpharmajournal.org/?p=22862

Introduction

The Nanoparticles (NPs) are a broad class of materials including particulate substances having a dimension less than 100 nm at least.¹ Noble metals like Silver in metal Nanoparticles mainly have been used for experimental purposes because of their robust properties in optics. This creates large amount of applications in areas such as photography, dentistry, electronics, food industries, clothing etc.² The shape and size of metal nanoparticle is measured typically using discrete techniques such as Scanning Electron Microscopy, Transmission Electron Microscopy etc.³

In the last decade an increasing use of artificial intelligence tools was observed in nanotechnology research. Artificial Intelligence can be used in classification of material properties of nanoscale, designing, simulation, nanocomputing etc. ⁴ Artificial neural network (ANN) is an efficient as well as dynamic simulation tool which allows one to classify, predict or estimate relationships among inputs and outputs.² They can expertly solve difficult problems such as stock exchange prediction, image compression, face recognition etc. These tasks may be carried out without any prior information.

Artificial Neural Network

An ANN is a computational technique that uses the assistance of a learning paradigm along with processing nodes and attempts to present an affiliation between the input and output data.⁵ Majorly, there are two learning paradigms that an ANN can employ; supervised learning and unsupervised learning.⁶

A basic ANN network comprises of three primitive layers; input layer, hidden layer and output layer as illustrated in Fig. 1. These layers contain various mathematical functions, nodes which are also called artificial neurons, associated with weights or coefficients that builds the structure of the neural network.⁷ When an input and the corresponding target is provided to the ANN model (the training in this case is supervised), the error is calculated from the difference between the system output and the target response. This information of the error is fed back (Back propagation or BP learning) during the training phase and consequently the weights are adjusted accordingly, thereby improving the system parameters. Reiteration is done until the desired performance is achieved.⁸

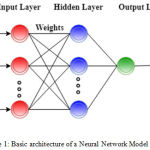Figure 1: Basic architecture of a Neural Network Model.   Click here to View figure

 

Several types of ANNs have been designed with different configurations either with a single-layer or multiple layer neurons. A multilayer perceptron (MLP) is the best model for complex problems. By introducing more number of hidden layers a MLP outlives the drawback of the single-layer perceptron. In a conventional feed-forward MLP network, the input responses are multiplied with the weights and these multiplied signals from each input are then summed and guided to a transfer function which gives the output result for that particular neuron.⁷

Learning Algorithms

There are several types of training algorithms that can be adopted to train an ANN. MATLAB provides 9 different types of algorithms for an Engine Data Set problem, out of which top 7 algorithms are explored in this study.

Conjugate Gradient

Conjugate Gradient (CG) starts by searching the negative of the descent in their first iteration. Before the next search is determined, a line search is implemented for acquiring the prime distance to travel forth the existing search direction, so that the two search directions are conjugate. The novel search direction is determined when the new steepest descent direction and the preceding search direction are combined.⁹ Several versions of CG are determined by computational means of the constant, β_k.⁶

Powell/Beale Restarts (traincgb)

Powell/Beale (CGB) technique will restart if the current and previous gradient have very little orthogonality between them.⁹

Fletcher-Reeves Update (traincgf)

For the Fletcher-Reeves Update (CGF), the constant is calculated as the ratio of the norm squared of the present gradient to the norm squared of the previous gradient.⁷

Polak-Ribiére Update (traincgp)

Another practice of the CG algorithm is Polak-Ribiére Update (CGP). In CGP, the constant is calculated by the inner product of the previous gradient change with the current gradient divided by the norm squared of the previous gradient. CGP requires more storage than CGF.⁶

Scaled Conjugate Gradient (trainscg)

Scaled Conjugate Gradient (SCG) does not call for a line search at each and every iteration and employs the step size scaling mechanism which reduces the time consumption, making SCG the fastest among the second order algorithm. Although the number of iteration may increase for the algorithm to converge.⁹

Quasi-Newton

Newton’s technique provides improved optimization and converges faster than CG techniques but the Hessian matrix of the performance index at the present values of the biases as well as weights, which is the elementary step to the Newton’s method, takes more time hence making the method complex for feed forward ANN. Based on this a class of algorithms, quasi-Newton or secant method, does not require the computation of second derivatives. In each iteration of the algorithm the approximate Hessian Matrix is updated.⁶

Broyden–Fletcher–Goldfarb–Shanno (trainbfg)

In Broyden–Fletcher–Goldfarb–Shanno (BFGS), the approximate Hessian matrix is stored with an n x n dimension, where n represents the number of weights and biases in the ANN model. Although it converges in fewer iterations, it has more calculations and storage requirements than CG methods.^7,9

One Step Secant Algorithm (trainoss)

The One Step Secant (OSS) technique adopts that at every iteration, the preceding Hessian matrix is the identity matrix thereby not storing the complete Hessian giving it an additional benefit of calculating the new search direction without calculating the matrix inverse.⁶

Levenberg-Marquardt (trainlm)

The Levenberg-Marquardt (LM) training algorithm is a numerical least-squares non-linear function minimization technique.¹⁰ LM method computes a Jacobian matrix that contains first derivatives of the network error with respect to the weights as well as biases. The calculation of Jacobian matrix by standard BP technique is less complicated than the Hessian matrix.⁶

LM algorithm first initializes the weights of the network following the computation of the outputs and errors for all the input responses. Subsequently, the Jacobian matrix is calculated and the new weights are obtained. A new error value is determined from these weights and a comparison between the new and the current error value is carried out. Accordingly, the regularization parameter, µ is reduced by a factor of β if error is smaller otherwise it is increased by β. It is re-iterated until the error is below the predefined value or a stopping condition is met.¹⁰

Other types of algorithms used are Variable Learning Rate (traingda, traingdx) and Resilient Backpropagation (trainrp).6

Network Design

Data Set

In this study, the sample data employed to train the ANN model is presented in [2, Table I]. The database is split into; training set, validating set and testing set. A training set is adopted for learning to fit the parameters and is specifically applied to alter the varying weights and errors of the network in each iteration.^2,11 Validation set tunes the parameters. It is used to vary and enhance the structure of ANN like training function, transfer function, number of hidden layers and neurons etc.^2,11 A test set is used only to assess the effectiveness and efficiency of the ANN.² Table [2, I] presents the four parameters produced as a function to predict the size of the Ag-NPs along with the actual size of the nanoparticle obtained.

Table 1: Experimental Values For Prediction Of The Size Of Ag-Nps.

S.No.	Volume. C. Longa Extract (mL)	Temperature (°C)	Stirring Time (h)	Volume of AgNO3(mL)	Ag-NPs Particle Size (Actual)(nm)
Training Set
1.	20	40	48	5	5.52
2.	20	50	48	10	6.08
3.	20	70	24	20	7.35
4.	10	25	24	1	8.18
5.	10	30	24	2	8.41
6.	10	60	12	15	9.35
7.	10	70	12	20	9.78
8.	5	25	24	1	10.46
9.	5	40	12	5	10.86
10.	5	70	6	20	11.82
11.	2	25	6	1	12.37
12.	2	30	6	2	12.49
13.	2	40	3	5	12.73
1.	2	50	3	10	12.96
15.	2	70	3	20	13.78
16.	1	25	3	1	14.36
17.	1	30	1	2	14.55
18.	1	40	1	5	14.65
19.	1	50	1	10	14.85
20.	1	70	1	20	15.32
Validating Set
21.	20	30	48	2	5.18
22.	10	50	24	10	9.11
23.	5	60	6	15	11.69
24.	2	60	3	15	13.47
25.	1	60	1	15	14.93
Testing Set
26.	20	25	24	1	4.90
27.	20	60	48	15	6.67
28.	10	40	24	5	8.85
29.	5	30	12	2	10.74
30.	5	50	6	10	11.23

 

Methodology

An appropriate ANN model requires a learning algorithm, transfer function, suitable number of hidden layers and neurons. The framework to build and elect the appropriate ANN model for the chosen application is shown in Fig. 2. The most common learning in ANN is the BP technique which uses a supervised learning. A supervised learning paradigm compares the output response to the target response to calculate the learning error. This learning error is used to adjust the network parameters to enhance the performance of the network.⁵ In this paper, the designed network has four input parameters and one output parameter. Thus, the ANN is constructed with 4 neurons in the input layer and the output layer with 1 neuron. The number of neurons in the hidden layer and the transfer function is tested against to find the best suitable architecture for the application. The final evaluation of each network operation is done using Mean Square Error (MSE), Mean Absolute Error (MAE), Error Sum of Squares (SSE) and Regression (R).

The values of these indices can be calculated using the following equations,

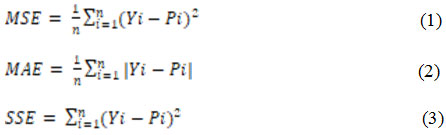
Where, n is the number of points, Yi is the value predicted from the ANN model and Pi is the actual value.² R, the determination coefficient of linear regression, is a line between the predicted values from the ANN model and the target output. It fits better to the actual data when the R value tends to 1.¹²

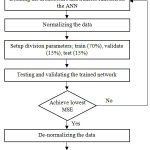Figure 2: Flowchart of the methodology used.   Click here to View figure

 

Results and Discussions

All 7 algorithms used are coded in MATLAB with R2012b (8.0.0.783) version.  The study is carried out by choosing one input, hidden and an output layer. The architecture of the ANN model is changed by altering the number of neurons in the hidden layer (10, 20, and 30) along with the transfer functions (purelin, logsig and tansig) in both hidden and output layer. Table II presents the values obtained by various architectures and transfer function arrangements of each algorithm. Normalization of all the input data in accordance with the transfer function is the first step of the calculation before using the neural networks. The last step is the de-normalization of the output data.² For enhanced performance and selecting the optimum architecture for the application, the performance indicators ((1)-(3)) and R between the target response and the output obtained are analyzed.

Table 2: Results And Comparison Of Algorithms Using Different Architectures And Transfer Functions.

Algorithm	Training Function	H	Transfer Function		Best Validation at Epoch	Epoch	R on Training	R on Validation	R on Testing
			Hidden	Output
Conjugate Gradient	traincgb	10	logsig	purelin	0.0033 at epoch 14	20	0.9864	0.9877	0.9711
			logsig	logsig	0.0582 at epoch 16	22	0.8845	0.9633	0.9969
			logsig	tansig	0.0099 at epoch 12	18	0.9815	0.9697	0.9649
			tansig	purelin	0.0245 at epoch 7	13	0.9740	0.8949	0.9554
			tansig	logsig	0.0027 at epoch 7	13	0.9753	0.9807	0.9802
			tansig	tansig	0.0021 at epoch 10	16	0.9791	0.9977	0.8021
		20	logsig	purelin	0.0022 at epoch 31	37	0.9942	0.9915	0.9942
			logsig	logsig	0.054 at epoch 21	27	0.8904	0.9408	0.9457
			logsig	tansig	0.0226 at epoch 3	9	0.9263	0.9901	0.9967
			tansig	purelin	0.0195 at epoch 12	18	0.9925	0.8846	0.9703
			tansig	logsig	0.0026 at epoch 26	32	0.9687	0.9941	0.9043
			tansig	tansig	0.0031 at epoch 7	13	0.9855	0.9975	0.9556
		30	logsig	purelin	0.0029 at epoch 11	17	0.9800	0.9892	0.9901
			logsig	logsig	0.0053 at epoch 10	25	0.8769	0.9189	0.9645
			logsig	tansig	0.0439 at epoch 4	10	0.9556	0.9353	0.9667
			tansig	purelin	0.0024 at epoch 34	40	0.9969	0.9886	0.9398
			tansig	logsig	0.0233 at epoch 15	21	0.9521	0.8570	0.9058
			tansig	tansig	0.0620 at epoch 5	11	0.9674	0.7895	0.9405
	traincgf	10	logsig	purelin	0.0014 at epoch 15	21	0.9880	0.9981	0.9784
			logsig	logsig	0.0022 at epoch 28	34	0.9077	0.9805	0.8597
			logsig	tansig	0.0376 at epoch 12	18	0.9278	0.9710	0.9496
			tansig	purelin	0.0030 at epoch 22	28	0.9905	0.9869	0.9605
			tansig	logsig	0.0122 at epoch 7	13	0.8446	0.9763	0.9576
			tansig	tansig	0.0056 at epoch 17	23	0.9921	0.9963	0.9871
		20	logsig	purelin	0.0021 at epoch 11	17	0.9748	0.9805	0.9729
			logsig	logsig	0.0563 at epoch 11	17	0.8751	0.9625	0.8621
			logsig	tansig	0.0419 at epoch 17	23	0.9844	0.9325	0.9494
			tansig	purelin	0.0067 at epoch 17	23	0.9694	0.9557	0.9883
			tansig	logsig	0.0075 at epoch 5	11	0.8501	0.9856	0.9855
			tansig	tansig	0.0456 at epoch 2	8	0.9355	0.9439	0.9823
		30	logsig	purelin	0.0057 at epoch 6	12	0.9776	0.9891	0.9697
			logsig	logsig	0.0109 at epoch 15	21	0.9228	0.8781	0.8880
			logsig	tansig	0.3116 at epoch 10	16	0.9444	0.9129	0.8875
			tansig	purelin	0.0179 at epoch 43	49	0.9943	0.9211	0.9739
			tansig	logsig	0.05417 at epoch 9	15	0.9145	0.9727	0.9466
			tansig	tansig	0.0152 at epoch 6	12	0.9748	0.9746	0.9537
	traincgp	10	logsig	purelin	0.0020 at epoch 9	15	0.9679	0.9922	0.9927
			logsig	logsig	0.0700 at epoch 2	3	0.90502	0.8122	0.8055
			logsig	tansig	0.0206 at epoch 25	31	0.9848	0.9788	0.9905
			tansig	purelin	0.0142 at epoch 6	12	0.9437	0.9612	0.9716
			tansig	logsig	0.0036 at epoch 16	22	0.9924	0.9824	0.9634
			tansig	tansig	0.0190 at epoch 2	8	0.9204	0.9852	0.8885
		20	logsig	purelin	0.0245 at epoch 6	12	0.96421	0.9669	0.954
			logsig	logsig	0.0117 at epoch 5	11	0.90012	0.8776	0.8624
			logsig	tansig	0.0383 at epoch 16	22	0.9648	0.9761	0.8404
			tansig	purelin	0.0144 at epoch 13	19	0.9787	0.9465	0.9966
			tansig	logsig	0.0090 at epoch 9	15	0.9696	0.9914	0.9392
			tansig	tansig	0.0171 at epoch 9	15	0.9677	0.9962	0.9835
		30	logsig	purelin	0.004 at epoch 8	14	0.9777	0.98295	0.86807
			logsig	logsig	0.0516 at epoch 9	15	0.8800	0.98295	0.8680
			logsig	tansig	0.1150 at epoch 5	11	0.9097	0.9547	0.9543
			tansig	purelin	0.0112 at epoch 22	28	0.9936	0.9039	0.9850
			tansig	logsig	0.0399 at epoch 45	51	0.9970	0.7896	0.928
			tansig	tansig	0.01950 at epoch 9	15	0.9890	0.9885	0.9848
	trainscg	10	logsig	purelin	0.0017 at epoch 18	24	0.9852	0.9917	0.9808
			logsig	logsig	0.0372 at epoch 13	19	0.9109	0.9056	0.8883
			logsig	tansig	0.0112 at epoch 17	23	0.9831	0.9925	0.8805
			tansig	purelin	0.0010 at epoch 12	18	0.9882	0.9885	0.9932
			tansig	logsig	0.0176 at epoch 26	26	0.7811	0.9223	0.9363
			tansig	tansig	0.0612 at epoch 17	23	0.9806	0.9985	0.9007
		20	logsig	purelin	0.0025 at epoch 22	28	0.9843	0.9897	0.9264
			logsig	logsig	0.0042 at epoch 12	18	0.8961	0.9898	0.9918
			logsig	tansig	0.0385 at epoch 12	18	0.9618	0.9428	0.9344
			tansig	purelin	0.0050 at epoch 47	53	0.999	0.9554	0.9797
tansig			logsig	0.0746 at epoch 16	21	0.8717	0.8212	0.8214
tansig			tansig	0.037 at epoch 10	16	0.9785	0.9782	0.9802
30		logsig	purelin	0.0031 at epoch 14	20	0.9844	0.9793	0.9679
		logsig	logsig	0.0056 at epoch 12	18	0.9055	0.9891	0.9556
		logsig	tansig	0.0614 at epoch 7	13	0.8326	0.9154	0.8425
		tansig	purelin	0.0380 at epoch 7	13	0.9321	0.8106	0.9403
		tansig	logsig	0.0055 at epoch 8	14	0.9033	0.8995	0.8428
		tansig	tansig	0.1157 at epoch 12	18	0.9405	0.9755	0.9374
quasi-Newton	trainbfg	10	logsig	purelin	0.0016 at epoch 21	27	0.9920	0.9663	0.9917
			logsig	logsig	0.0440 at epoch 7	13	0.8967	0.8775	0.9213
			logsig	tansig	0.0282 at epoch 22	28	0.9757	0.977	0.9918
			tansig	purelin	0.0069 at epoch29	35	0.9961	0.9538	0.9941
			tansig	logsig	0.0367 at epoch 18	24	0.8885	0.9245	0.9792
			tansig	tansig	0.0142 at epoch 26	32	0.9820	0.9817	0.9786
		20	logsig	purelin	0.0063 at epoch 25	31	0.9896	0.9625	0.9624
			logsig	logsig	0.0103 at epoch 9	15	0.9003	0.9195	0.9395
			logsig	tansig	0.486 at epoch 17	23	0.9906	0.9308	0.8701
			tansig	purelin	0.0195 at epoch 33	39	0.9969	0.9450	0.8070
			tansig	logsig	0.0422 at epoch 21	27	0.8890	0.8934	0.9289
			tansig	tansig	0.0019 at epoch 18	24	0.9846	0.9965	0.9578
		30	logsig	purelin	0.0028 at epoch 26	32	0.9955	0.9708	0.9906
			logsig	logsig	0.0086 at epoch 15	21	0.9106	0.9682	0.8964
			logsig	tansig	0.0070 at epoch 18	24	0.9572	0.9811	0.83
			tansig	purelin	0.0022 at epoch 6	12	0.9664	0.9821	0.8168
			tansig	logsig	0.0083 at epoch 7	13	0.8214	0.9959	0.9455
			tansig	tansig	0.01 at epoch 4	10	0.9209	0.9851	0.9926
	trainoss	10	logsig	purelin	0.0024 at epoch 12	18	0.97948	0.9947	0.97729
			logsig	logsig	0.01568 at epoch 7	13	0.9164	0.9802	0.97626
			logsig	tansig	0.0186 at epoch 15	21	0.9835	0.9477	0.9428
			tansig	purelin	0.0076 at epoch 7	13	0.9731	0.9663	0.9337
			tansig	logsig	0.0109 at epoch 3	9	0.9009	0.9118	0.9434
			tansig	tansig	0.0322 at epoch 4	10	0.9603	0.9877	0.9173
		20	logsig	purelin	0.002 at epoch 34	40	0.9838	0.9881	0.9745
			logsig	logsig	0.0574 at epoch 27	33	0.9009	0.8239	0.95261
			logsig	tansig	0.0316 at epoch 13	19	0.9658	0.9579	0.9547
			tansig	purelin	0.0045 at epoch 75	81	0.9931	0.9492	0.9996
			tansig	logsig	0.0059 at epoch 4	10	0.8050	0.9429	0.9677
			tansig	tansig	0.0803 at epoch 10	16	0.9554	0.8986	0.9422
		30	logsig	purelin	0.0035 at epoch 17	23	0.97342	0.98861	0.98923
			logsig	logsig	0.0993 at epoch 13	19	0.8720	0.96933	0.8588
			logsig	tansig	0.0196 at epoch 3	9	0.9402	0.9858	0.9810
			tansig	purelin	0.0157 at epoch 29	35	0.9933	0.8529	0.9927
			tansig	logsig	0.048 at epoch 6	12	0.8102	0.9907	0.9165
			tansig	tansig	0.0534  at epoch 35	41	0.9807	0.9444	0.9630
Levenberg-Marquardt	trainlm	10	logsig	purelin	0.0008 at epoch 15	21	0.9977	0.9968	0.9959
			logsig	logsig	0.0020 at epoch 15	21	0.9060	0.9803	0.9163
			logsig	tansig	0.0144 at epoch 11	17	0.9994	0.9913	0.9863
			tansig	purelin	0.0033 at epoch 2	8	0.9871	0.9943	0.9764
			tansig	logsig	0.005 at  epoch 5	11	0.9132	0.9876	0.8244
			tansig	tansig	0.0037 at epoch 10	16	0.9972	0.9975	0.9853
		20	logsig	purelin	0.0016 at epoch 2	8	0.9986	0.9981	0.9800
			logsig	logsig	0.0121 at epoch 2	8	0.9087	0.9234	0.9166
			logsig	tansig	0.0410 at epoch 2	8	0.9409	0.9337	0.8826
			tansig	purelin	0.0023 at epoch 2	8	0.9910	0.9957	0.9934
			tansig	logsig	0.0091 at epoch 149	149	0.9405	0.8253	0.8044
			tansig	tansig	0.0095 at epoch 11	17	0.9979	0.9364	0.8362
		30	logsig	purelin	0.0036 at epoch 6	10	0.9998	0.9669	0.9375
			logsig	logsig	0.0036 at epoch 5	11	0.9217	0.9675	0.9916
			logsig	tansig	0.1298 at epoch 1	7	0.8216	0.945	0.9853
			tansig	purelin	0.0040 at epoch 3	6	0.9991	0.9744	0.8632
			tansig	logsig	0.012 at epoch 8	14	0.8805	0.9335	0.9389
			tansig	tansig	0.0168 at epoch8	14	0.9990	0.9985	0.9953

 

Other values of the indices comprising MSE, MAE and SSE are recorded in Fig. 3, 4 and 5. The transfer function is applied to both hidden and output layer in the ANN model. Therefore for example, in Fig. 3. (2-1) explains the use of Logsig transfer function in the hidden layer and Purelin transfer function in the output layer. All the other combinations follow the same pattern.

The values of indices are computed using the MATLAB syntax in the code itself. As presented in Table II, the optimum network model for this application for traincgb is when the network has 10 neurons in the hidden layer and logsig; purelin as the activation function in the network. The MSE corresponding to this is 0.003. It can be seen that all the other readings for MSE are bigger than MSE reading for the optimum network found. The R values for this network are 0.9864, 0.9877 and 0.9711. For traincgf the optimum network is found to be 10, logsig; purelin with MSE value as 0.027 and R value as 0.9880, 0.9981 and 0.9784 whereas traincgp gives the optimal results when the network architecture and parameters are set to 10, tansig; logsig where MSE value is seen to be 0.0026 and R values as 0.9924, 0.9824 and 0.9634. The trainscg algorithm gives better results with 10, tansig; purelin as its architecture and activation function. The MSE value for the same is found to be 0.0028. 0.9882, 0.9885 and 0.9932 are the R values. However, it is seen that MSE values for trainbfg algorithm, 0.0018, is same for when the network is 10, logsig; purelin and 10, tansig; purelin. In this case, the optimal network is chosen by comparing the R values and the best validation giving the most favorable architecture in trainbfg as 10, logsig; purelin with best validation performance being 0.0016 at epoch 21 and 0.9920, 0.9663, 0.9917 being the R values. In trainoss the finest value of MSE is 0.0027 whereas R is 0.9838, 0.9881, 0.9745 with the network parameters as 20, logsig; purelin. Finally for trainlm, MSE value is recorded as 0.00007 with R values nearest to 1; 0.9977, 0.9968 and 0.9959 when the network had 10 number of neurons in the hidden layer and logsig; purelin as the activation function.

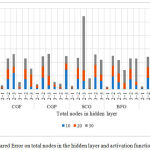Figure 3: Effect of Mean Squared Error on total nodes in the hidden layer and activation function on each algorithm.   Click here to View figure

 

Effect of each of the seven algorithms on the output response by varying the architecture of the ANN model and the transfer function in hidden and output layer is shown in Fig. 3, 4 and 5. ANN models that are simulated using numerous training functions are altered in accordance with the number of neurons in their hidden layer. MSE of all the responses recorded is illustrated in Fig. 3. MSE is an important criterion for measuring the overall performance of a designed ANN model. Fig. 4 illustrates a graph between the MAE and total number of nodes in the hidden layer and activation function for all the 7 algorithms used to design the various ANN models. The absolute value of the difference between the target value provided to the ANN model to train and the actual value obtained is the absolute error. Fig. 5 illustrates a graph between error sum of squares, which computes the total deviation of the obtained values from the fitting line or the regression line, and total number of nodes in the hidden layer and activation function. Smaller the value of SSE, better will be the regression line. It is sometimes also referred to as residuals sum of square.

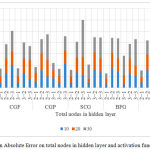Figure 4: Effect of Mean Absolute Error on total nodes in hidden layer and activation function on each algorithm.   Click here to View figure

 

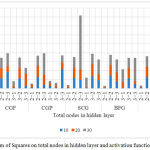Figure 5: Effect of Error Sum of Squares on total nodes in hidden layer and activation function on each algorithm.   Click here to View figure

 

Conclusion

In this research, the size of the Ag-NPs is determined using ANN modeling from different combinations of architectures and transfer functions by means of a feed-forward neural network model which renders the effect of volume of C. longa extraction, stirring time, temperature, and volume of AgNO3 on the nanocomposites behavior. The ANN model is simulated, trained and tested with the learning algorithms like Quasi-Newton, Conjugate Gradient and Levenberg-Maquardt using the dataset. In the projected work it is evident that Levenberg-Maquardt is the best suited algorithm when considering engine data set type for the particular application. It converges in lesser epochs and indeed takes shorter time period than all the other training algorithms. Some suitable architectures gave worthy performances within the same algorithms as their R value is observed nearest to 1. The experiment shows that ANN is an effectual tool in pondering subjects related to nanoengineering as the size of the silver nanoparticle is predicted in the absence of the costly and time-consuming tests.

Acknowledgement

The authors would like to acknowledge & thank Dr. V. Ganapathy, Professor in SRM Institute of Science & Technology, Kattankulathur for his immense help in this work.

References

1. Khan I.,  Saeed K., S khan I. Nano particles Properties applications and toxicities.  Arabian Journal of Chemistry. 2017. Available: http://dx.doi.org/ 10.1016/j.arabjc. 2017.05.011.
2. Shabanzadeh,  Senu N.,  Shameli K.,  Ismail F.  Application of Artificial Neural Network (ANN) for Prediction Diameter of Silver Nano particles Bio synthesized in Curcuma Long a Extract. Digest Journal of Nano materials and Bio structures. 2013;8(3):1133–1144.
3. Steven J. O.  Silver Nano particles Properties and Applications Sigma-Aldrich, Available: https://www. sigmaaldrich.com/technical-documents/articles/materials-science/nano materials/silver-nano particles .html. Accessed. 2018;16.
4.  Sacha G. M.,  Varona P. Artificial intelligence in nanotechnology. Nanotechnology. 2013;24:452002.
   CrossRef
5. Hemmat M.  E.,  Afranda M.,  Wongwisesb S., Naderic A.,  Asadid A.,  Rostamia S.,  Akbaria M. Applications of feed forward multi layer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg(OH)2–EG using experimental data. International Communications in Heat and Mass Transfer. 2015;67;46–50.
   CrossRef
6.  Demuth H., Beale M., Hagan M . Neural Network Toolbox^TM 6 User’s Guide, COPYRIGHT. Available. 1992–2008. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.144.5444&rep=rep1&type=pdf.
7.  Sharma B., Venugopalan K. Comparison of Neural Network Training Functions for Hematoma Classification in Brain CT Images. IOSR Journal of Computer Engineering (IOSR-JCE). 2014;16(1):31-35.
   CrossRef
8.  Dongare D.,Kharde R. R., Amit D. K.  Introduction to Artificial Neural Network.  International Journal of Engineering and Innovative Technology (IJEIT). 2012;2(1):189-194.
9.  Richard J. S.  An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, edition 1 , Carnegie Mellon University, Pittsburgh, August 1994. Available: https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf. Accessed. 2018;March 17.
10. El-Nabarawy I., Ashraf M. A., Donald C. W. I.  Levenberg-Marquardt and Conjugate Gradient Methods Applied to a High-Order Neural Network, The 2013 International Joint Conference on Neural Networks (IJCNN), Dallas TX. 2013;1-7.
11.  Brownlee J.  What is the Difference Between Test and Validation Datasets – Machine Learning Mastery, [Online]. Available https://machine learning mastery.com/difference-test-validation-datasets/. Accessed. 2018; March 17.
12. Shyam S. S., Oon-Doo B.,  Marcotte M. Neural networks for predicting thermal conductivity of bakery products. Journal of Food Engineering. 2002;52(3):299-304.
    CrossRef

(Visited 369 times, 1 visits today)