Sapana Singh Yadav and Usha Chouhan

Department of Bioinformatics, Maulana Azad National Institute of Technology Bhopal, India.

Corresponding Author E-mail: sapanasy9@gmail.com

DOI : https://dx.doi.org/10.13005/bpj/1470

Abstract

Laminopathy is a group of rare genetic disorders, including EDMD, HGPS, Leukodystrophy and Lipodystrophy, caused by mutations in genes, encoding proteins of the nuclear lamina. Analysis of protein interaction network in the cell can be the key to understand; how complex processes, lead to diseases. Protein-protein interaction (PPI) in network analysis provides the possibility to quantify the hub proteins in large networks as well as their interacting partners. A comprehensive genes/proteins dataset related to Laminopathy is created by analysing public proteomic data and text mining of scientific literature. From this dataset the associated PPI network is acquired to understand the relationships between topology and functionality of the PPI network. The extended network of seed proteins including one giant network consisted of 381 nodes connected via 1594 edges (Fusion) and 390 nodes connected via 1645 edges (Coexpression), targeted for analysis. 20 proteins with high BC and large degree have been identified. LMNB1 and LMNA with highest BC and Closeness centrality located in the centre of the network. The backbone network derived from giant network with high BC proteins presents a clear and visual overview which shows all important proteins of Laminopathy and the crosstalk between them. Finally, the robustness of central proteins and accuracy of backbone are validated by 248 test networks. Based on the network topological parameters such as degree, closeness centrality, betweenness centrality we found out that integrated PPIN is centred on LMNB1 and LMNA. Although finding of other interacting partners strongly represented as novel drug targets for Laminopathy.

Keywords

Betweenness Centrality; Closeness Centrality; Laminopathy; Protein-protein Interaction network (PPIN)

Download this article as: 

Copy the following to cite this article: Yadav S. S, Chouhan U. Analysis of Protein-Protein Interaction Network of Laminopathy Based on Topological Properties. Biomed Pharmacol J 2018;11(2).

Copy the following to cite this URL: Yadav S. S, Chouhan U. Analysis of Protein-Protein Interaction Network of Laminopathy Based on Topological Properties. Biomed Pharmacol J 2018;11(2). Available from: http://biomedpharmajournal.org/?p=20800

Introduction

Laminopathies, a group of rare genetic disorders caused by mutations in genes, encoding proteins of the nuclear lamina. Patients with classical laminopathy have mutations in the gene coding for lamin A/C (LMNA gene). Mutations in lamin B (LMNB2 gene) reported recently.¹ In addition to providing structural support to the nucleus, lamins also contributes to nucleo-cytoskeletal coupling, cell cycle regulation, cell apoptosis, chromatin organization, DNA replication, transcriptional regulation and responses to oxidative stress.² The nuclear envelope entered the medical area in the mid-1990s, when mutations in emerin were identified in patients with Emery-Dreifuss muscular dystrophy.³ The LMNA gene, encoding all A-type nuclear lamins, was linked to EDMD a few years later^4,5 and links between nuclear structure and human disease have been studied extensively since then in labs throughout the world.

Biological networks can be used to describe biological interactions such as the atomic interactions occurring between protein structures, the interactions of metabolites and proteins during specific cellular events such as the cell cycle and, on a macroscopic level, the interrelationships between organisms in an ecosystem.^6,7 Systems approaches aim to develop an understanding of the inter-relationships between proteins, metabolites or other molecules across organisms.⁸ Modern high-throughput techniques, taking measurements on a system-wide level, are well suited to the global analysis and modelling of networks for different diseases.^9,10,11 In comparison to wet lab techniques, computational methods have the potential to reduce noise and systematic errors.¹² Protein complexes are remarkable for understanding principles of cellular organization and function.⁸ High throughput experimental techniques have generated a large amount of protein interactions, which makes it doable to uncover protein complexes from protein protein interaction networks.^13,14 A PPI network (PPIN) can be modelled as an undirected graph, where vertices stand for proteins and edges represent interactions between proteins.¹⁵ Protein complexes are set of proteins that interact with one another, typically dense subgraphs in PPI networks.^14,16 To reveal the significance of the laminopathy disease, insilico based methodology have been used to identify the key proteins and their interactor. The integration of proteins interface structure into interaction graph models gives a better explanation of hub proteins, and builds up the relationship between the role of the hubs in the cell and their topological properties.^17,18 In this study, the interactions among the proteins have been implemented to produce and analyse a giant network by the topological analysis of the PPIN derived from the genes/proteins related to Emery-Dreifuss muscular dystrophy(EDMD),^4,19 Hutchinson-Gilford Progeria Syndrome (HGPS),^20-22 Leukodystrophy²³ and Lipodystrophy.²⁴ Different bioinformatics tools related to the proposed methodology are implemented to construct the PPI network of candidate genes and analyzed the topological properties like degree, betweenness centrality (BC) and closeness centrality (CC).¹⁷

Method

Research methods used in this study mainly included five steps, first step: Extraction of candidate genes, second step: Construction of PPIN of the seed proteins, third step: Merging of all PPIN scanned from seed proteins, fourth step: Analysis of the giant PPIN according to topological properties, fifth step: Acquiring backbone network.

Extraction of the Candidate Genes

Extraction of the candidate genes related to EDMD, HGPS, Leukodystrophy and Lipodystrophy disease done by PolySearch text mining systems²⁵ and NCBI database, which are web-based text mining system for extracting relationships between human diseases, genes, mutations, drugs and metabolites system and produce relevant information regarding individual query. As a result, 245 candidate genes associated with examining diseases obtained. To check the accuracy, the association of genes with disease is manually confirmed, and sorted the genes on the basis of Z score. The threshold for candidate genes set as Z score > 0. Finally, total 88 candidate genes are obtained, Table 1.

Table 1: The list of genes extracted from NCBI and PolySearch Text mining system database showing association with Progeria, EDMD, Leukodystrophy and Lipodystrophy

S.No.	Symbol	Description	S.No.	Symbol	Description
HGPS
1	BANF1	Barrier To Autointegration Factor 1	45	LMNB1	Lamin B1
2	C myc	Avian Myelocytomatosis	46	MAG	Myelin associated glycoprotein
3	DDX12	DEAD/H (Asp-Glu-Ala-Asp/His) box polypeptide 12, pseudogene	47	MT-ND5	Mitochondrially encoded NADH dehydrogenase 5
4	ELN	Elastin	48	NDUFAF2	NADH dehydrogenase (ubiquinone) complex I, assembly factor 2
5	EMD	Emerin	49	NDUFAF4	NADH dehydrogenase (ubiquinone) complex I, assembly factor 4
6	ERCC1	Excision repair cross-complementing rodent repair deficiency, complementation group 1	50	NDUFS1	NADH dehydrogenase (ubiquinone) Fe-S protein 1,
7	ERCC4	Excision repair cross-complementing rodent repair deficiency, complementation group 4	51	NDUFS2	NADH dehydrogenase (ubiquinone) Fe-S protein 2,
8	ROBO3	Roundabout, Axon Guidance Receptor, Homolog 3	52	NDUFS7	NADH dehydrogenase (ubiquinone) Fe-S protein 7,
9	LMNA	Lamin A/C	53	NDUFV1	NADH dehydrogenase (ubiquinone) flavoprotein 1, 51kDa
10	MMP20	Matrix Metallopeptidase 20	54	NUBPL	Nucleotide binding protein-like
11	SIRT1	Sirtuin 1	55	PLP1	Proteolipid protein 1
12	SUN2	Sad1 and UNC84 domain containing 2	56	POLR3A	Polymerase (RNA) III (DNA directed) polypeptide A
13	WRN	Werner syndrome,RecQ helicase-like	57	POLR3B	Polymerase (RNA) III (DNA directed) polypeptide B
14	ZMPSTE24	Zinc metallopeptidase STE24	58	POU2F1	POU class 2 homeobox 1
EDMD					59
15	BCLAF1	BCL2-associated transcription factor 1	60	SOX10	SRY (sex determining region Y)-box 10
16	EMD	Emerin	61	ST8SIA4	ST8 alpha-N-acetyl-neuraminide alpha-2,8-sialyltransferase 4
17	LMNA	Lamin A/C	62	SUMF1	Sulfatase modifying factor 1
18	SUN2	Sad1 and UNC84 domain containing 2	63	TREX1	Three prime repair exonuclease 1
19	SYN1	Synapsin I	64	TUBB4	Tubulin, beta 4A class Iva
20	SYN2	Synapsin 2	LIPODYSTROPHY
21	TMEM43	Transmembrane protein 43	65	AGPAT2	1-acylglycerol-3-phosphate O-acyltransferase 2
22	TMPO	Thymopoietin	66	BANF1	Barrier to autointegration factor 1
23	YTHDC1	YTH domain containing 1	67	BSCL2	Berardinelli-Seip congenital lipodystrophy 2 (seipin)
LEUKODYSTROPHY			68	CAV1	Cavolin 1, Cavolae protein
24	ACOX1	Acyl-CoA oxidase 1, palmitoyl	69	CIDEC	Cell death-inducing DFFA-like effector c
25	AIMP1	Aminoacyl tRNA synthetase complex-interacting multifunctional protein 1	70	ENSG0000235715	–
26	ARSA	Arylsulfatase A	71	FBN1	Fibrillin 1
27	ARSB	Arylsulfatase  B	72	FOS	FBJ murine osteosarcoma viral oncogene homolog
28	ASPA	Aspartoacylase	73	GLMN	Glomulin, FKBP associated protein
29	C8orf38	Chromosome 8 Open Reading Frame 38	74	LMF1	Lipase maturation factor 1
30	C17orf68	Chromosome 17 Open Reading Frame 68	75	LMNA	Lamin A
31	C20orf7	Chromosome 20 Open Reading Frame 7	76	LMNB2	Lamin B2
32	CLCN2	Chloride channel, voltage-sensitive 2	77	LPIN1	Lipin1
33	EIF2B1	Eukaryotic translation initiation factor 2B, subunit 1 alpha	78	LPIN2	Lipin2
34	EIF2B2	Eukaryotic translation initiation factor 2B, subunit 2 beta	79	LPIN3	Lipin3
35	EIF2B3	Eukaryotic translation initiation factor 2B, subunit 3 gamma	80	PIK3R1	Phosphoinositide-3-kinase, regulatory subunit 1
36	EIF2B4	Eukaryotic translation initiation factor 2B, subunit 4 delta	81	PLIN1	Perilipin1
37	EIF2B5	Eukaryotic translation initiation factor 2B, subunit 5 epsilon	82	POLD1	Polymerase (DNA directed), delta 1, catalytic subuni1
38	FA2H	Fatty acid 2-hydroxylase	83	PPARG	Peroxisome proliferator-activated receptor gamma
39	FAM126A	Family with sequence similarity 126, member A	84	PTRF	Polymerase I and transcript release factor
40	FOLR1	Folate receptor 1	85	RXRG	Retinoid X receptor, gamma
41	FOXRED1	FAD-dependent oxidoreductase domain containing 1	86	STAR	Steroidogenic acute regulatory protein
42	GALC	Galactosylceramidase	87	WRN	Werner syndrome,RecQ helicase-like
43	GFAP	Glial fibrillary acidic protein	88	ZMPSTE24	Zinc metallopeptidase STE24
44	GJC2	Gap junction protein, gamma 2

 

Construction of PPI Network of the Seed Proteins

Candidate genes are converted to seed proteins, for each protein a PPIN extracted from the STRING database.²⁶ Interactions in STRING are provided with a confidence score, and accessory information such as protein domains and 3D structures is made available, all within a stable and consistent identifier space. Fusion and coexpression attributes are fixed to construct the PPIN. Finally, we obtained different PPIN for different seed proteins.

Merging of all PPI Network Scanned from Seed Proteins

To merge all the PPIN of seed proteins within a single network called as extended network, Cytoscape v3.0.2 has been used,^27,28 it provides a platform to analyze and visualize the extended network Figure 1 (a,b). Extended network included different distinct sub network, according to clustering of the seed proteins. Among them, only one network has been considered with the highest existing nodes and edges for further analysis. Such network consists of maximum interactions among the seed proteins and termed as a giant network shown in Figure 2 (a,b). Other sub localized networks are to be ignored as they have less interaction.

Figure 1: Overview of the extended network. (a) Fusion: 581 nodes and 2270 edges. (b) Coexpression: 585 nodes and 2340 edges, includes one giant network and thirteen separated small networks   Click here to View figure

 

Figure 2: Topology of giant network (a) Fusion: 381 nodes and 1594 edges (b) Coexpression: 390 nodes, 1645 edges.   Click here to View figure

 

Analysis of the Giant PPI Network According to Topological Properties

PPI Network of relevant disease represented by an undirected graph G(V, E), where V represents the set of vertices in the graph G and E represents the set of edges.²⁹ NetworkAnalyzer, was used to compute various network parameters.³⁰ To predict and study the key nodes or hub proteins of the giant network topological parameters have been calculated. Therefore, after analyzing the giant network, according to each distinct attribute degree, BC and CC values for each node have been calculated. That helps in finding the proteins of central positions in the network, as they can be highly important from a functional point of view too. In undirected networks, the node degree of a node n is the number of edges linked to n.^29,31 The number of links of a node was observed to follow a power law distribution, that is, the probability of a node having degree k is proportional to k−γ, and the distribution is independent of the number of nodes; hence these networks are called scale free. Scale-free networks have many nodes with small degrees and allow nodes with high degrees (hubs) with decreasing probability.³¹ Betweenness measures how often nodes occur on the shortest paths between other nodes.³² For a graph G(V, E), with n vertices, the betweenness centrality C_B(v) a vertex v is defined as,

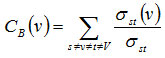
Where σ_st is the number of shortest paths from s to t, and σ_st(v) is the number of shortest paths from s to t that passes through a vertex v. Closeness centrality³³ C_c(n) of a node n is defined as the reciprocal of the average shortest path length and is computed as,

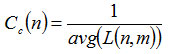
Where L(n,m) is the length of the shortest path between two nodes n and m. The closeness centrality of each node is a number between 0 and 1. In the PPIN the nodes with high degree defined as hub proteins and the nodes with high betweenness defined as bottleneck proteins.¹⁸

Acquiring Backbone Network

The proteins with high BC and degree should be profoundly used intersections, these proteins and links between them extracted from giant network, are called backbone network. To evolve a high BC range particular threshold fixed at 15% of the total nodes set of the network.^34,35 As the founding of Backbone Network by both fusion and coexpression attribute is almost similar, so fusion attribute has been chosen for further analysis. Total number of nodes in the giant network is 381(fusion) among them  20 proteins with high BC value have been chosen which are LMNB1, TERF2, LMNA, CAV1, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, EMD, EP300, KAT2B, PLIN1, AIMP1, AGPAT2, TGFB1, SRC, PPARGC1A to form backbone network Figure 3.

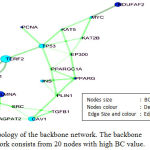Figure 3: Topology of the backbone network. The backbone network consists from 20 nodes with high BC value.   Click here to View figure

 

Results and Discussion

In this study, the effects and important role of individual protein/gene of related disease has been illustrated. The analysis depends on the kind of methodology applied to construct the merged network. The aim is to find out the contribution of these proteins to the pathogenesis of Laminopathy and discover other key proteins cooperating with them by topological analyses.

PPI Network

Using PolySearch Text mining tools and NCBI database, 14 candidate genes related to HGPS, 9 to EDMD, 41 to the Leukodystrophy and 24 to the Lipodystrophy have been obtained, Table 1. These candidate genes are converted to seed proteins and obtained their interacting partners from STRING database, a precomputed database for the exploration of PPI. Coexpression and fusion attributes of PPI have been chosen to analyse the merged network, so two different merged networks are generated. Fusion attribute has been considered first, as it is the most relevant attribute described in, for the analysis of disease PPIN. In this case the merged network with 581 nodes and 2270 edges shown in Figure 1(a), is a combination of thirteen different sub networks. LMNB1, DDX12, SIRT1, ROBO3, TGFB3, ELN, MMP20, ERCC1, TMEM43, YTHDC1, ARSA, EIF2B3, GALC, PLP1 are the seed proteins while playing the central role in each fourteen sub networks. These nodes are distributed in fourteen different clusters according to interaction possibility. The large network among them, in which LMNB1 playing the role of central protein, consists of 381 nodes and 1594 edges extracted as giant network shown in Figure 2(a). Similarly, considering the coexpression attribute the merged network consists of 585 nodes and 2340 edges and 14 subnetworks shown in Figure 1(b). It is notified that in all two cases foresaid seed proteins are playing the key role in each sub network. The giant network consists of 390 nodes and 1645 edges, according to coexpression attribute shown in Figure 2(b). Similar to fusion attributes in case of coexpression attribute LMNB1 is found as central protein of the giant network.

Key Nodes in the PPI Network

To predict and study the key nodes or hub proteins of the giant network, Topological parameters have been calculated with NetWorkAnalyzer. Three topological properties are essential to find out the key nodes of any network. Therefore, after getting the giant network, according to each distinct attribute the BC value of each node has to be measured and comparison can be made to find out the ascending order of the BC values. After calculation twenty proteins have been selected by a large BC value in case of fusion attributes they are LMNB1, TERF2, LMNA, CAV1, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, EMD, EP300, KAT2B, PLIN1, AIMP1, AGPAT2, TGFB1, SRC, PPARGC1A and these proteins form a backbone network. Among these proteins LMNB1 has highest BC value 0.287. TERF2, LMNA, CAV1, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, EMD, EP300, KAT2B, PLIN1, AIMP1, AGPAT2, TGFB1, SRC, PPARGC1A are other proteins with high BC and CC value, described in Table 2. The most interesting fact is that though TERF2, TP53, INS, PCNA, KAT5, EP300, KAT2B, TGFB1, SRC, PPARGC1A are having the high BC value but these proteins are not in the list of 88 seed proteins. Therefore, only ten proteins of the backbone network are in the list of seed proteins while having the highest BC value.

Table 2: List of high BC nodes and their CC values in giant network of (FUSION)

SN	NODE	BC	CC
1	LMNB1	0.287009	0.291562
2	TERF2	0.264808	0.236192
3	LMNA	0.26648	0.211383
4	CAV1	0.252828	0.185034
5	NDUFAF2	0.166011	0.181954
6	TP53	0.255548	0.179216
7	INS	0.246593	0.143685
8	MYC	0.191243	0.134733
9	PPARG	0.240202	0.131876
10	PCNA	0.211228	0.12723
11	KAT5	0.223136	0.11442
12	EMD	0.257627	0.110797
13	EP300	0.240964	0.11072
14	KAT2B	0.223925	0.106568
15	PLIN1	0.248204	0.104925
16	AIMP1	0.233846	0.102976
17	AGPAT2	0.247235	0.102683
18	TGFB1	0.21814	0.090545
19	SRC	0.237204	0.082378
20	PPARGC1A	0.246914	0.080442

 

Similarly for the giant network of coexpression attribute the topological result is obtained and summarized in Table 3, in which LMNB1 and LMNA are the highest BC value 0.28 and 0.26 proteins among the twenty proteins TERF2, CAV, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, UBC, EP300, PLIN1, KAT2B, AIMP1, AGPAT2, EMD, TGFB1, PPARGC1A with high BC according to threshold. While in both cases if we consider degree and CC parameter, then we observed that LMNB1 had a larger degree 60 and CC 0.287009, 56 and CC 0.288362 for fusion and coexpression attribute respectively, Table 4 and Table 5. These results are in agreement with experimental results obtained by earlier research workers.^2,3,5

Table 3: List of high BC nodes and their CC Values in giant network (COEXPRESSION)

SN	NODE	BC	CC
1	LMNB1	0.288362	0.28601
2	LMNA	0.271648	0.235578
3	TERF2	0.264806	0.23418
4	CAV1	0.255753	0.184785
5	NDUFAF2	0.164761	0.178153
6	TP53	0.253916	0.173889
7	INS	0.246671	0.139105
8	MYC	0.189756	0.131964
9	PPARG	0.24042	0.128324
10	PCNA	0.20993	0.124217
11	KAT5	0.2214	0.112157
12	UBC	0.245581	0.110331
13	EP300	0.239827	0.107364
14	PLIN1	0.249679	0.105244
15	KAT2B	0.222159	0.104436
16	AIMP1	0.234479	0.100686
17	AGPAT2	0.248721	0.09985
18	EMD	0.258988	0.097815
19	TGFB1	0.219898	0.088545
20	PPARGC1A	0.246984	0.077938

 

Table 4: List of large Degree nodes and their CC values (FUSION)

SN	NODE	DEGREE	CC
1	LMNB1	60	0.287009
2	NDUFS7	44	0.144597
3	NDUFS8	37	0.144542
4	NDUFAF2	36	0.166011
5	LMNA	34	0.26648
6	PPARG	33	0.240202
7	PCNA	33	0.211228
8	C20orf7	33	0.144377
9	AGPAT2	29	0.247235
10	SYNE1	29	0.265549
11	SYNE2	28	0.264993
12	BRCA1	27	0.24532
13	NDUFS2	27	0.144432
14	NDUFAF3	27	0.144103
15	NDUFA1	26	0.143939
16	AIMP1	25	0.233846
17	NDUFAF4	25	0.144049
18	FOXRED1	25	0.144049
19	EMD	24	0.257627
20	NDUFS1	23	0.144213

 

Table 5: List of large Degree nodes and their CC values (COEXPRESSION)

S.N.	NODE	DEGREE	CC
1	LMNB1	56	0.288362
2	NDUFS7	49	0.143595
3	LMNA	41	0.271648
4	NDUFS8	41	0.143542
5	NDUFAF2	37	0.164761
6	C20orf7	35	0.143384
7	PPARG	33	0.24042
8	PCNA	33	0.20993
9	NDUFS2	32	0.143437
10	NDUFV2	32	0.143278
11	NDUFA2	31	0.143067
12	FOXRED1	30	0.143067
13	AGPAT2	29	0.248721
14	NDUFV1	28	0.143225
15	NDUFS1	28	0.143225
16	AIMP1	26	0.234479
17	EMD	25	0.258988
18	NDUFAF4	25	0.143067
19	NDUFA1	25	0.142962
20	MT-ND1	25	0.126217

 

Sub-Network Consisting of All Shortest Paths Between the Candidate Genes

In general, for any arbitrary network, it is not necessary that each node can be connected to each other. But in case of PPIN of any disease the giant network consists of those nodes which can be connected directly or indirectly to each node. So the interaction between the nodes significantly depends on the shortest path length between these two nodes, the shortest path length gives a description about active interactions among the nodes. Again the high BC value of any node depends on the number of shortest paths passing through a specific node. Therefore the high BC value of any nodes implies, having more number of shortest paths.

The Robustness of the Backbone Network and LMNA as A Central Protein

As a result twenty proteins with the largest BC value in the test networks acquired are LMNB1, TERF2, LMNA, CAV1, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, EMD, EP300, KAT2B, PLIN1, AIMP1, AGPAT2, TGFB1, SRC, PPARGC1A. The occurrence of LMNB1 and LMNA is more frequent than the other nodes which have high BC value. Among the total of 248 test network, the number of frequency of LMNB1 in test network is 210. The accuracy of the backbone network is 0.75807. It is examined that whenever the number of omitting genes is larger than 3 then the accuracy of backbone networks and frequency of the LMNB1 and LMNA are decreased continuously. Accuracy of backbone network (Fusion attribute) given in Table 6.

Table 6: Frequency of nodes with the largest BC value and accuracy of backbone in the 248 test networks

Number of omitted genes	Frequency of nodes with the largest BC value in the test networks							Accuracy of the backbone	Number of the test networks
	LMNB1	LMNA	TERF2	CAV1	NDUFAF2	TP53	INS
1	88	0	0	0	0	0	0	0.78478	88
2	59	1	0	0	0	0	0	0.78206	60
3	14	4	1	0	1	0	0	0.76458	20
4	13	4	2	0	0	0	1	0.74654	20
5	13	4	1	1	0	0	1	0.74452	20
6	11	3	2	1	1	1	1	0.74255	20
7	12	4	3	0	1	0	0	0.74147	20
Summary	210	20	9	2	3	1	3	0.75807	248

 

Comparative Network Statics for Fusion and Coexpression

In this attempt the comparative analysis of the network was also performed, according to fusion and coexpression attributes to understand how the attributes can make an effect on our experimental disease network, is summarized in Table 7. The result of all the parameters has the same numeric value, only shortest path in case of coexpression is slightly higher which does not affect other parameters like BC value, CC value, clustering coefficient etc. in both cases we get LMNB1 as a central protein and same hub proteins.

Table 7: Comparative Network Statics For Fusion And Coexpression

S.N.	Network statics	Fusion	Coexpression
1	Clustering Coefficient	0.727	0.726
2	Network diameter	12	12
3	Network radius	6	6
4	Network centralization	0.072	0.071
5	Shortest paths	144780	151710
6	Characteristic path length	5.426	5.400
7	Avg. No.of neighbours	7.617	7.595
8	Number of nodes	381	390
9	Network density	0.02	0.02
10	Network heterogeneity	0.713	0.712

 

Graphical results of different topological parameters shown Figure 4 (a,b), explains the highest betweenness centrality in the giant network is approximate 0.3 and in that case the number of nodes is 60. This implies, the node having the highest betweenness value also having the highest number of neighbors which signifies evidences of the key node of the network. If we compare the second highest beetweenness value of the network, it is 0.25 (approx.) and consists of around 25 neighbors. Therefore the node having the first position in both cases of BC value and neighborhood, proving better candidature for the key role in extended merged giant network rather than the node having second position. NetworkAnalyzer can fit a power law to some topological parameters and follow the least squares method,³⁶ and only points with positive coordinate values are considered for the fit, gives the correlation between the given data points and the corresponding points on the fitted curve. In addition, the R-squared value (also known as coefficient of determination) is reported. This coefficient gives the proportion of variability in a data set, which is explained by a fitted linear model. Therefore, the R-squared value is computed on logarithmized data, where the power-law curve: y = β xα is transformed into linear model: ln y = ln β + α ln x., here correlation between the data points and corresponding points on the line is approximately 0.528 and 0.480, R-squared value is 0.258 and 0.257 respectively for fusion and coexpression.

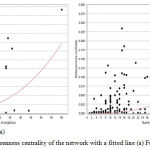Figure 4: Betweenness centrality of the network with a fitted line (a) Fusion (b) Coexpression     Click here to View figure

 

Figure 5 (a,b), Graphical representation of the number of nodes in a giant network, according to degrees, graph shows the distribution of those nodes which are following minimum number of  connectivity i.e. nodes are connected by at least one edge. Here we identified that when the number of nodes are 70 then  the degree of such nodes is 10. Also, we observed that in some cases where the number of degrees was high, the number of nodes were less. This implies such nodes are not part of giant network and they made subnetwork which contains less nodes. Therefore the connectivity is high, but the node is less. NetworkAnalyzer provides another useful feature – fitting a line on the data points of some complex parameters. The method applied is the least squares method for linear regression.³⁷ Fitting a line can be used to identify linear dependencies between the values of the x and y coordinates in a complex parameter. Figure 5 shows the fitted line on degree, having correlation between the data points and corresponding points on the line is approximately 0.607 and 0.463, R-squared value is 0.719 and 0.700 respectively for fusion and coexpression.

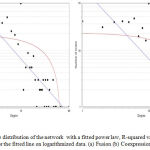Figure 5: Node Degree distribution of the network  with a fitted power law, R-squared value reported is the R-squared value for the fitted line on logarithmized data. (a) Fusion (b) Coexpression   Click here to View figure

 

Figure 6 (a,b), explains the value of  closeness centrality of each node of the giant network, according to the number of neighbors. Clearly, it shows that only single node consists of highest CC value which is 0.28 approximate worth having 38 neighbors and graph also fitted to power law having corelation between data points and corresponding point on the line is approximately 0.237 and 0.238, R-squared value is 0.430 and 0.423. From similar concept, it is possible to conclude that this particular node can play the key role in the network.

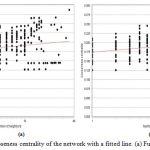Figure 6: Closeness centrality of the network with a fitted line. (a) Fusion (b) Coexpression   Click here to View figure

 

Conclusion

In present study, we created a comprehensive initial dataset of genes statistically related to Laminopathy and a further expansion through the construction of related PPIN. Here we studies relationships between interacting proteins according to topological properties. We show that a protein or a hub of proteins can play an important role to interact with other proteins and also extend the PPI disease network. Again, it is possible to find out the key proteins, which are main mediator for two or more disease networks. Identifying such hub of proteins can help to understand the mechanism of pathways also it might be possible to emphasize that they have high functional importance in the cell. Most of seed proteins associated with Laminopathy and their PPI neighbors are connected to a giant network, which is analyzed by using different centrality indexes for hubs detection. Our findings suggested that Laminopathy disease mechanism and pathway is organized by an integrated PPI network centered on LAMIN gene product LMNA and LMNB1 proteins, while other proteins TERF2, LMNA, CAV1, NDUFAF2, TP53, INS, MYC, PPARG, PCNA, KAT5, EMD, EP300, KAT2B, PLIN1, AIMP1, AGPAT2, TGFB1, SRC, PPARGC1A with high BC values predict their significant role in a network. Also the analysis of backbone network presented a clear overview of all important genes, their related regulatory pathways for Laminopathy. The backbone network is robust against the changes of initial seed genes. The results may provide a basis for further experimental investigations to study PPI networks associated with Laminopathy and other relevant disease.

Acknowledgements

The authors are cordially thankful to the Madhya Pradesh Council of Science and Technology, Bhopal for providing financial support to carry out this work.

Conflict of Interest

There is no conflicts of interest

References

1. Davidson PM, Lammerding J. Broken nuclei – lamins, nuclear mechanics and disease. Trends in cell biology. 2014. doi:10.1016/j.tcb.2013.11.004.
   CrossRef
2. Burke B, Stewart CL. The laminopathies: the functional architecture of the nucleus and its contribution to disease. Annu Rev Genomics Hum Genet. 2006;7:369-405.
   CrossRef
3. Bione S, Maestrini E, Rivella S, Mancini M, Regis S, Romeo G, and Toniolo D. Identification of a novel X-linked gene responsible for Emery-Dreifuss muscular dystrophy. Nat. Genet. 1994;8, 323–327.
   CrossRef
4. Bonne G, Di Barletta M.R, Varnous S, Be cane H.M, Hammouda E H, Merlini L, Muntoni F, Greenberg, C. R, Gary F, Urtizberea J A, et al., Mutations in the gene encoding lamin A/C cause autosomal dominant Emery-Dreifuss muscular dystrophy. Nat. Genet. 1999;21,285–288.
   CrossRef
5. Schreiber K, Kennedy B. When Lamins Go Bad: Nuclear Structure and Disease.Cell. 2013;152:1365–1375
   CrossRef
6. Bruggeman FJ and Westerhoff HV. The nature of systems biology. Trends in Microbiology. 2007;15:45–50.
   CrossRef
7. Alm E and Arkin A. Biological networks. Current Opinion in Structural Biology. 2003;13:193–202.
   CrossRef
8. Barabasi AL and Oltvai Z. Network biology: understanding the cell’s functional organization. Nature Reviews Genetics. 2004;5:101–113.
   CrossRef
9. Shruti Mishra and Debahuti Mishra. An Overview of Biological Networks: Mechanisms, Methodologies And Applications. Int J Pharm Bio Sci. 2016;7(3):979 –988.
10. Ran J, Li H, Fu J, Liu L Xing YLi X , Shen H, Chen Y, Jiang X, Li Y and Li H. Construction and Analysis of the Protein Protein Interaction Network Related to Essential Hypertension. BMC Systems Biology. 2013;7(32):1752-0509.
    CrossRef
11. LaCount DJ, Vignali M, Chettier R, Phansalkar A, Bell R, et al., A protein interaction network of the malaria parasite Plasmodium falciparum. Nature. 2005;438:103–107
    CrossRef
12. Gilchrist M A, Salter L A, and Wagner A. A statistical framework for combining and interpreting proteomic datasets. Bioinformatics.2004;20:689–700.
    CrossRef
13. Raman K. Construction and analysis of protein-protein interaction networks. Autom Exp, 2010;2:2.
    CrossRef
14. Zhang Y, Lin H, Yang Z, Wang J. Integrating experimental and literature protein-protein interaction data for protein complex prediction. 2015;2:4. doi: 10.1186/1471-2164-16-S2-S4.
    CrossRef
15. Ryan DP, Matthews JM. Protein-protein interactions in human disease. Curr Opin Struct Biol. 2005;15(4):441-446.
    CrossRef
16. Sam L, Liu Y, Li J, Friedman C, Lussier YADiscovery of protein interaction networks shared by diseases. Pacific Symposium on Biocomputing. 2007;12:76-87.
17. Doncheva N T, Assenov Y, Domingues S F and Albercht M. Topological Analysis and Visualization of Biological Networks and Protein Structures. Nature Protocols. 2012;7,670–685 doi:10.1038/nprot.2012.004.
    CrossRef
18. Xu J, Li Y. Discovering disease-genes by topological features in human protein-protein interaction network. Bioinformatics. 2006;22:2800-2805.
    CrossRef
19. Anne Helbling-Leclerc, Gisele Bonne and Ketty Schwartz. Emery-Dreifuss muscular dystrophy. European Journal of Human Genetics. 2002;10,157-161.
    CrossRef
20. Eriksson M, Brown T W, Gordon L B, Glynn M W, Singer J, ScottL, Erdos M R, Robbins C M, Moses T Y, Berglund P, Dutra A, Pa E, Drukin S, Csoka A B, Boehnke M, Glover T W, and Collins F S. Recurrent De Novo Point Mutations In Lamin A Cause Hutchinson-Gilford Progeria Syndrome. Nature. 2003;423,293-298.
    CrossRef
21. Scaffidi P, and Misteli T. Reversal of the cellular phenotype in the premature aging disease Hutchinson-Gilford progeria syndrome. Nature Medicine. 2005;11(4);440-445.
    CrossRef
22. Goldman R. D, Shumaker D. K, Erdos M. R, Eriksson M, Goldman A. E, Gordon L. B, Gruenbaum Y, Khuon S, Mendez M and Collins F. S.  Accumulation of mutant lamin A causes progressive changes in nuclear architecture in Hutchinson-Gilford progeria syndrome. Proc. Natl. Acad. Sci. 2008;101(24);8963-8968.
    CrossRef
23. Quasar S. Padiath, Kazumasa Saigoh, Raphael Schiffmann, Hideaki Asahara, et al., Lamin B1 duplications cause autosomal dominant leukodystrophy. 2006; doi:10.1038/ng1872.
    CrossRef
24. Huang I, Sleigh A, Rochford J. J and Savage D. B. Lipodystrophy: metabolic insights from a rare disorder. J Endocrinol. 2010; 207245-255.
25. Cheng D, Knox C, Young N, Stothard P, Damaraju S, Wishart D. PolySearch: a web-based text mining system for extracting relationships between human diseases, genes, mutations, drugs and metabolites. 2008; doi: 10.1093/nar/gkn296.
    CrossRef
26. Mering C, Jensen LJ, Snel B, Hooper SD, Krupp M, Foglierini M, Jouffre N, Huynen MA, Bork P. STRING: known and predicted protein protein associations, integrated and transferred across organisms. Nucleic Acids Res. 2005;433-437.
27. Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: A Software Environment for Integrated Models of Biomolecular Interaction Networks. Genome Res. 2003;13(11):2498-2504.
    CrossRef
28. Cline MS, Smoot M, Cerami E, Kuchinsky A, Landys N, Workman C, et al., Integration of biological networks and gene expression data using Cytoscape. 2007; doi:10.1038/nprot.2007.324
    CrossRef
29. A K Dwivedi and Usha Chouhan. Simulated Annealing Model For Reticulate Evolution In Molecular Sequences. Int J Pharm Bio Sci. 2013;4(4):497-503.
30. N T Doncheva, Y Assenov, F S Domingues, M lbrecht. Topological analysis and interactive visualization of biological networks and protein structures Nature Protocols. 2012;7:670–685. doi:10.1038/nprot.2012.004.
    CrossRef
31. Diestel R. Graph theory. Springer-Verlag. Heidelberg. 2005;3-540-26182-6.
32. Barabasi A.L and Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512.
    CrossRef
33. Brandes U.A faster algorithm for betweenness centrality. J Math Sociol. 2001;25:163-177.
    CrossRef
34. Newman M. EJA measure of betweenness centrality based on random walks. arXiv condmat/0309045, 2003.
35. Goni J, Esteban FJ, de Mendizabal NV, Sepulcre J, Ardanza-Trevijano S, Agirrezabal I, Villoslada P. A computational analysis of protein-protein interaction networks in neurodegenerative diseases. BMC Syst Biol. 2008;2:52.
    CrossRef
36. Kim KK, Kim HB. Protein interaction network related to Helicobacter pylori infection response. World J Gastroenterol. 2009;15:4518–4528.
    CrossRef
37. Weisstein E. W. Least Squares Fitting-Power Law. MathWorld – A Wolfram Web Resource.(http://mathworld.wolfram.com/LeastSquaresFittingPowerLaw.html).