Vikrant Singh Thakur1, Shubhrata Gupta2 and Kavita Thakur3
1Department of Electrical Engineering. National Institute of Technology, Raipur India. 2Department of Electrical Engineering. National Institute of Technology, Raipur India. 3S. O. S in Electronics, Pt. Ravishankar Shukla University Raipur, India. Corresponding Author Email: vikrant.st@gmail.com
DOI : https://dx.doi.org/10.13005/bpj/634
Abstract
Image compression is dissimilar than compressing other unprocessed binary data. Obviously, general purpose compression techniques deliberated for raw binary data can be used to compress images, but the result is not the finest one, because of the variations in statistical property of image. Statistical properties of image must be completely exploit by encoders to obtained efficient image compression. The most popular transform coder was developed by the Joint Photographic Experts Group (JPEG), which utilizes fixed block size discrete cosine transform (DCT) to obtain image data decorrelation. With fixed block size DCT, JPEG has no independent control over quality and bit rate simultaneously. Human visual system is less sensitive to quantization noise in high-activity areas of an image than in low-activity areas. That means the threshold of visibility of quantization noise is higher in areas with details than in flat areas. this is the key, why not exploit human visual system’s weakness to achieve much higher compression with good visual quality by hiding as much quantization noise in busy areas as possible. It is indeed possible by using DCT with varying block sizes and quantizing busy areas heavily and flat areas lightly. To apply variable block size DCT transform on an image, quad tree decomposition technique is commonly used. In quad tree decomposition technique a square block is divides in smaller blocks, if the difference between maximum and minimum pixel values exceeds a threshold. This threshold selection plays a very crucial role, because the independent selection of threshold value without considering the statistical properties of the input image, may lead to even worst compression characteristics. To address this difficulty, this paper proposes a novel optimum global thresholding based variable block size DCT coding for efficient image compression. The proposed method calculates the required threshold value for blocks decomposition using optimum global thresholding technique, which exploits the edge characteristics of the image. Comparison has been made with baseline fixed block size DCT coder by using mean square error (MSE), peak signal to noise ratio (PSNR) and compression ratio (CR) as criterions. It is shown that the variable block size DCT transform coding system using proposed optimum global thresholding technique has better MSE and highly improved PSNR and CR performance for all test images.
Keywords
Variable block size DCT; quad-tree decomposition; optimum global threshold; MSE; CR; PSNR
Download this article as:| Copy the following to cite this article: Thakur V. S, Gupta S, Thakur K. Optimum Global Thresholding Based Variable Block Size DCT Coding For Efficient Image Compression. Biomed Pharmacol J 2015;8(1) |
| Copy the following to cite this URL: Thakur V. S, Gupta S, Thakur K. Optimum Global Thresholding Based Variable Block Size DCT Coding For Efficient Image Compression. Biomed Pharmacol J 2015;8(1). Available from: http://biomedpharmajournal.org/?p=1667 |
Introduction
In the past few decades, transform coding has been used widely in compressing image and video data [1, 2, 3]. A typical transform coding system [4] divides an input image into fixed size square blocks. The frequently used block sizes are 8×8 or 16×16. At the transmitter, every block is transformed by an orthogonal transform. The DCT is regularly preferred because of its high potential of energy compaction and its fast computational algorithm. The transform coefficients are then quantized and coded for transmission. At the receiver, the process is inverted to obtain the decoded image. In most existing transform coding systems like JPEG, the block size used to divide an input image is fixed. This approach, however, has not taken into account, that image statistics may be inhomogeneous and may vary from area to area in an image. Some areas of an image can have only soft changes and contain no large contrast edge. In these areas, larger compression can be obtained by using a larger block size. However, some areas contain high activities and contrast edges, smaller block size transform, must be used to gain better visual quality [1]. Therefore, to truly adapt to the internal statistics of an image in different areas, a transform coding system ought to vary the block size to give up a better tradeoff between the bit rate and the quality of decoded image. Generally speaking, if a segment of an image contains high activities, the segment should be partitioned into smaller areas. This process continues until the divided segments have homogeneous statistics or only smooth changes.
In [5], an adaptive transform coding system using variable block size was proposed. The system uses a mean-difference based criterion to determine whether a block contains high contrast edges or not. If a block contains high contrast edges, the block is divided into four smaller blocks and the process repeats with the divided blocks until the four blocks contain no further high contrast edges or the smallest block size is reached.
In [7], a classified vector quantization (CVQ) of an image, based on quad trees and a classification technique in the discrete cosine transform (DCT) domain was proposed. They have obtained decoded images of good visual quality for encoding rates of 0.3 and 0.7 bpp.
In [8], this work describes a progressive image transmission (PIT) scheme using a variable block size coding technique in conjunction with a variety of transform domain quantization schemes. The developed scheme utilized a region growing technique to partition the images so that regions of different sizes can be addressed using a small amount of side information. Simulation results shown that the reconstructed images preserve fine and pleasant qualities based on both subjective and mean square error criteria.
In [9] an edge-oriented progressive image coding scheme using a hierarchical edge extraction was presented. This scheme is based on the two-component model, that is, edges and smooth component. It is shown through the simulations that the proposed scheme results in performance improvements over MPEG-2 I-picture coding in terms of both the subjective quality and signal-to-noise ratio.
In [10] variable image segmentation and mixed transform were used to capitalize on the narrow band and broadband signal components for image compression. A gain of around 1.7-5 dB in PSNR over conventional JPEG was reported by authors.
This paper proposes a novel optimum global thresholding based variable block size DCT coding for efficient image compression. The proposed method calculates the required threshold value for blocks decomposition using optimum global thresholding technique, which exploits the edge characteristics of the image. Comparison has been made with baseline fixed block size DCT coder by using Mean Square Error (MSE) and compression ratio (CR) as criterions. It is shown that the variable block size DCT transform coding system using proposed optimum global thresholding technique has better MSE, PSNR and CR performance for all test images. In next section, the fixed and variable block size DCT transform coding system is briefly described. The proposed optimum global thresholding based variable block size DCT coding, is then defined in next section. To compare the performance of the system using two different criteria, Results and discussion section gives the simulation result obtained for three images coded at the quality factor 5. Finally, last section is the conclusion.
Fixed and Variable Block Size Dct Image Coding
Fixed Block Size DCT Image Coding
In case of fixed block size DCT coding, to apply the DCT, the input image is divided into 8´8 blocks of pixels. If the width or height of the input image is not divisible by 8, the encoder must make it divisible. The 8´8 blocks are processed from left-to-right and from top-to-bottom [11].
The purpose of the DCT is to transform the value of pixels to the spatial frequencies. These spatial frequencies are extremely linked to the level of detail present in an image. High spatial frequencies provide high levels of detail, while lower frequencies give lower levels of detail. The mathematical definition of DCT is [11, 19, and 20]:
Forward DCT:
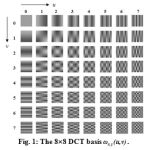 |
Figure 1: The 8´8 DCT basis ωx,y(u,v). |
The transformed 8´8 block now consists of 64 DCT coefficients. The very first coefficient F(0,0) is the DC component and the next 63 coefficients are AC component. The DC component F(0,0) is basically the sum of the 64 pixels in the input 8´8 pixel block multiplied by the scaling factor (1/4)C(0)C(0)=1/8 as shown in equation 3 for F(u,v).
The next step in the compression process is to quantize the transformed coefficients. Each one of the 64 DCT coefficients are uniformly quantized [11, 14, and 15]. The 64 quantization step-size parameters for uniform quantization of the 64 DCT coefficients form an 8´8 quantization matrix. Every element in the quantization matrix is an integer values between ranges 1 to 255. Each DCT coefficient F(u,v) is divided by the corresponding quantizer step-size parameter Q(u,v) in the quantization matrix and then rounded to the nearest integer as:
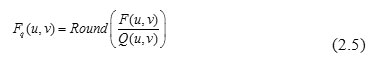
The JPEG standard does not define any fixed quantization matrix. It is the choice of the user to select a quantization matrix. There are two structures of the quantization matrices provided in JPEG standard. These two quantization matrices are shown below:
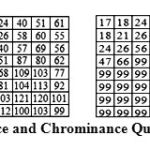 |
Figure 2: Luminance and Chrominance Quantization matrix. |
The quantization process has the key role in the JPEG compression. It is the procedure which removes the high frequencies present in the input image. Quantization is used because of the fact that the eye is much more sensitive to lower spatial frequencies than to higher frequencies of the transformed image. This is performed by dividing values at high indexes in the vector (the amplitudes of higher frequencies) with larger values than the values by which are divided the amplitudes of lower frequencies. The larger values in the quantization table is the larger error introduced by this lossy process, and the smaller visual quality [12].
Variable Block Size DCT Image Coding
Previous subsection, briefly dealt with transform coder with fixed DCT block size. With fixed block size DCT, the coder doesn’t have independent control over quality and bit rate simultaneously. Human visual system is less sensitive to quantization noise in high-activity areas of an image than in low-activity areas. That means that the threshold of visibility of quantization noise is higher in areas with details than in flat areas. In this case the basic idea is to exploit our own visual system’s weakness to achieve much higher compression with good visual quality by hiding as much quantization noise in busy areas as possible. It is indeed possible if we use DCT with varying block sizes and quantize busy areas heavily and flat areas lightly [12].
One possible method is to start with an N × N block with N = 2m, m being a positive integer. Typically, N is 16 or 32. Using the block variance as the metric, we can decompose the N × N block into four blocks. Each block, in turn, may be subdivided further into four blocks depending on the variance metric. This process of subdividing may be continued until left with 2 × 2 sub blocks. This is the familiar quad tree decomposition.
Once the quad tree decomposition is done, DCT can be applied to each sub block and the DCT coefficients quantized using suitable quantization matrices. DCTs of smaller blocks may be quantized rather heavily and of bigger sub blocks lightly to achieve higher compression without sacrificing the quality. This is feasible because smaller blocks were obtained on the basis of the variance; smaller blocks have higher variances than bigger blocks. Therefore, quantization noise will be less visible in those smaller sub blocks due to the human visual response [12].
Optimum Global Thresholding
Thresholding may be considered as a statistical-decision theory problem whose objective is to minimize the average error incurred in assigning pixels to two or more groups (also called classes).
The approach of optimum global thresholding is also known as Otsu’s method. The method is optimum in the sense that it maximizes the between-class variance, a famous measure used in statistical discriminant analysis. The basic idea is that thresholded classes must be distinct with respect to the intensity values of their pixels and, conversely, that a threshold giving the best separation between classes in terms of their intensity values would be the best (optimum) threshold. Besides to its optimality, Otsu’s method has the important property that it is, based entirely on computations performed on the histogram of an image, an easily obtainable 1-D array [13].
Let denote the L distinct intensity levels in a digital image of size pixels, and let , denote the number of pixels with intensity i. The algorithm of the optimum global thresholding technique is given as [13]:
- Determine the normalized histogram of the input image. Denote the components of histogram by , for .
- Determine the cumulative sums, , for given as
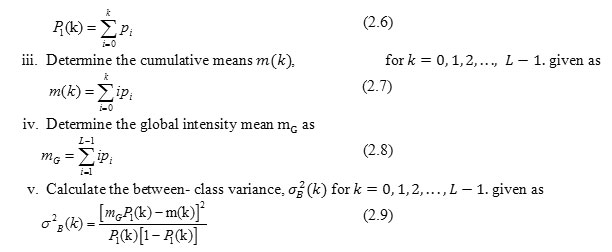
6. Obtain the Otsu threshold, as the value of k for which σB2(k) is maximum. If the unique maximum is not available, obtain k* by averaging the values of k corresponding to the various maxima detected.
7. Obtain the separability measure, η* evaluating following at k = k* .

where σ2G (k) is the global variance.
Proposed Optimum Global Thresholding Based Variable Block Size Dct Coding
This section briefly presents the proposed optimum global thresholding based variable block size DCT image coding system. The proposed system starts with the use of quad tree decomposition, to divide an input image into sub blocks of size between 2×2 and 16×16 pixels. The block decomposition used here is based on the homogeneity of pixels in a block. The quad tree decomposition divides a square block if the difference between maximum and minimum pixel values exceeds a threshold (say T). Otherwise, the block is not divided further. The range of the threshold for block decomposition is . This threshold selection plays a very crucial role, because the independent selection of threshold value without considering the statistical properties of the input image, may lead to even worst compression characteristics.
To address this difficulty, this work utilized optimum global thresholding, to calculate the optimum threshold T, which leads accurate decision about the blocks division in sub blocks. Once the image is quad decomposed, the sub blocks are DCT transformed, DCT coefficients are quantized and dequantized, and finally inverse DCT transformed.
For the 8×8 blocks, the proposed work uses the default JPEG luma quantization matrix and quantizer scale. For the 2×2 and 4×4 blocks, heavy quantization is used, and for the 16×16 blocks, light quantization is used be used. The DC coefficient of the 2×2 and 4×4 blocks is quantized using a step size of 8. The AC coefficients of 2×2 blocks are quantized using a step size of 34, while those of 4×4 blocks are quantized using 24 as the step size. The DC coefficient of the 16×16 blocks is quantized with a step size of 4 and all AC coefficients of the 16×16 blocks is quantized with a step size of 16. The complete process involved in the proposed coder is shown in figure (3), with the help of block diagram representation.
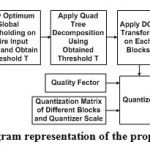 |
Figure 3: Block diagram representation of the proposed image coder. |
Results and Discussions
The proposed work has been successfully implemented and simulated on MATLAB 2012b. Simulation is carried out to compare the fixed block size DCT coding (FBSDCT) and proposed optimum globally threshold based variable block size DCT coding (OGTBVBSDCT) systems. The input image has resolution of 8 bits per pixel and the image size is . The largest and smallest block sizes allowed are 16×16 and 2×2 respectively. The decision threshold T is obtained optimum global threshold technique and the quality scale is fixed to 5. 50 images, has been used for comparative analysis, few of them (test images) have been shown in from Fig. 4.1 to Fig. 4.5. For the comparative analysis the three well known parameters compression ratio (CR), mean square error (MSE) and peak signal to noise ratio have been used. The resultant images obtained after using FBSDCT, and OGTBVBSDCT have been shown in Table-1.
 |
Table 1: The resultant images obtained after using FBSDCT and proposed OGTBVBSDCT techniques for quality value Q = 5. |
 |
Figure 4 |
 |
Figure 5 |
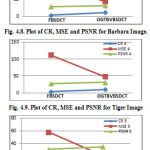 |
Figure 6 |
Now the values of compression ratio (CR), mean square error (MSE) and peak signal to noise ratio (PSNR), obtained after image compression using FBSDCT and proposed OGTBVBSDCT image coding systems for all the input images shown from Fig. 4.1 to Fig. 4.5, have been tabulated in Table-2 and are plotted in Fig. 4.6 to Fig. 4.10.
Table 2: Values of CR, MSE and PSNR for all five test images
| Images | Parameters | FBS-
DCT |
Proposed OGTBVBS-
DCT |
Threshold Value (T) Obtained Using Optimum Global Thresholding |
| Lena Image | CR1 | 3.3572 | 12.0515 | 0.4627 |
| MSE1 | 89.386 | 31.1507 | ||
| PSNR1 | 28.618 | 33.1961 | ||
| Football Image | CR2 | 5.1449 | 11.2085 | 0.3882 |
| MSE2 | 77.937 | 29.192 | ||
| PSNR2 | 29.213 | 33.4782 | ||
| Barbara Image | CR3 | 3.0181 | 11.274 | 0.4392 |
| MSE3 | 99.356 | 43.2813 | ||
| PSNR3 | 28.158 | 31.7678 | ||
| Tiger Image | CR4 | 2.9805 | 9.7495 | 0.4353 |
| MSE4 | 112.19 | 48.0093 | ||
| PSNR4 | 27.631 | 31.3176 | ||
| Pears Image | CR5 | 3.7758 | 13.9706 | 0.502 |
| MSE5 | 57.947 | 20.5174 | ||
| PSNR5 | 30.500 | 35.0096 |
 |
Table 2 B |
It is clearly observable from Table-II and Fig. 4.6 to Fig. 4.10, that the developed technique OGTBVBSDCT provides much higher compression ratio as compared to available FBSDCT system. Close observation of obtained results revels that, due to utilization of variable block size DCT with efficiently calculated threshold “T” using optimum global threshold technique, enables the developed image coder to greatly reduce the blocking artifacts during decompression, clearly reflected by the higher value of CR, PSNR and lower value of MSE in the plots, which was not the case of available FBSDCT system. Hence the developed is able to obtain efficient image compression than the available FBSDCT system.
Conclusions
In this paper a novel optimum global thresholding based variable block size DCT coding for Efficient Image compression has been successfully implemented using MATLAB. The proposed method calculates the required threshold value for blocks decomposition efficiently using optimum global thresholding technique, which exploits the edge characteristics of the image. This process is very crucial, because lower values of threshold “T” leads to higher number of block decomposition and higher values of “T” leads to smaller or non decomposition of blocks.
Most often higher value of “T” tends to convert variable block size DCT to fixed block size DCT. Therefore appropriate value of “T” must be required to maintain efficiency of block decomposition. A complete comparative analysis of the proposed system, based on 50 standard image database(out of which five image comparisons are included in this paper), with baseline fixed block size DCT coder by using mean square error (MSE), peak signal to noise ratio (PSNR) and compression ratio (CR) as criterions, is also presented in the result section.
It is shown that the variable block size DCT transform coding system using proposed optimum global thresholding technique has better MSE and highly improved PSNR and CR performance for all test images. The proposed coding system OGTBVBSDCT has achieved four times more compression ratio (CR) and restricted the MSE to fifty percent as that obtained for the available FBSDCT system. Hence the developed optimum global thresholding based variable block size DCT coding system (OGTBVBSDCT) provides efficient image compression than the available fixed block size DCT coding system (FBSDCT). The proposed method can be further improved using various optimization techniques to get more refined threshold value for blocks decomposition.
References
- Chun-tat See; Wai-Kuen Cham, “An adaptive variable block size DCT transform coding system,” International Conference on Circuits and Systems, 1991. Conference Proceedings, China. 1991, pp.305, 308 vol.1, 16-17 Jun 1991.
- N. Netravali and J.O. Limb, ‘Picture Coding: A Review’, Proc. IEEE, vo1.68, no.3. Pp.366-406. Mar.1980.
- K. Jain, ‘Image Data Compression: A Review’, Proc. IEEE, vo1.69, 110.3, pp.349-389, Mar.1981.
- -H. CHEN and W.K. PRATT, ‘Scene Adaptive Coder’, IEEE Trans. Comm., VoLCOM-32, No.3, pp.225-232, March 1984.
- Cheng-Tie CHEN, ‘Adaptive Transform Coding Via Quadtree Based Variable Block size DCT’, International Conference on ASSP, pp.1854-1857, 1989.
- K.CHAM and R.J.CLARKE, ‘DC Coefficient Restoration in Transform Image Coding’, IEE Proc., Vo1.131, part F, pp.709-713, Dec.1984.
- Lee,M.H.; Crebbin,G.”Classified vector quantization with variable block -size DCT models” Vision, Image and Signal Processing, IEE Proceedings, vol. no. 141, Issue: 1, pp 39 – 48, 1994.
- Huh,Y. ; Panusopone,K. ; Rao,K.R. “Variable block size coding of images with hybrid quantization” IEEE Transactions on Circuits and Systems for Video Technology, pp. 679 – 685 vol.6, issue. 6, 1996.
- Itoh, Y. “An edge-oriented progressive image coding” IEEE Transactions on Circuits and Systems for Video Technology, pp. 135 – 142 vol.6, issue. 2, 1996.
- Verma, S.; Pandit, A.K., “Quad tree based Image compression,” TENCON 2008 – 2008 IEEE Region 10 Conference , vol., no., pp.1,4, 19-21 Nov. 2008.
- Wallace, G.K., “The JPEG still picture compression standard,” IEEE Transactions on Consumer Electronics, vol.38, no.1, pp. xviii, xxxiv, Feb 1992.
- S. Thyagarajan “Still Image and Video Compression with MATLAB”1st edition, Wiley Publications.
- C. Gonzalez and R E Woods “Digital Image Processing” 2nd edition, Prentice Hall Publications.
- Thakur, V. S.; Thakur, K., “Design and Implementation of a Highly Efficient Gray Image Compression Codec Using Fuzzy Based Soft Hybrid JPEG Standard,” International Conference on Electronic Systems, Signal Processing and Computing Technologies (ICESC), 2014, pp.484,489, 9-11 Jan. 2014.
- Thakur, N. K. Dewangan, K. Thakur ” A Highly Efficient Gray Image Compression Codec Using Neuro Fuzzy Based Soft Hybrid JPEG Standard ” Proceedings of Second International Conference “Emerging Research in Computing, Information, Communication and Applications” ERCICA 2014, vol.no.1, pp. 625-631, 9-11 Jan. 2014.
- Berg and W. Mikhael, “An efficient structure and algorithm for the mixed transform representation of signals”, 29th Astomar Conference on Signals, Systems and Computers, vol.2 no.5, pp.1056-1060, 1995.
- Ramaswamy and W. B. mikhael, “A mixed transform approach for efficient compress of medical images”, IEEE Trans. Medical Imaging vol.15, no3, pp.343-352, june1996.
- Melnikov and A. K. Katsaggelos, “A Jointly Optimal Fractal /DCT Compression scheme” IEEE Transactions on Multimedia, Vol4, No.4, pp.413-22, Dec 2002.
- Sung-Ho Bae; Munchurl Kim, “A Novel Generalized DCT-Based JND Profile Based on an Elaborate CM-JND Model for Variable Block-Sized Transforms in Monochrome Images,” IEEE Transactions on Image Processing, , vol.23, no.8, pp.3227,3240, Aug. 2014.
- Krishnamoorthy, R.; Punidha, R., “An orthogonal polynomials transform-based variable block size adaptive vector quantization for color image coding,” IET Image Processing, , vol.6, no.6, pp.635,646, August 2012.








