Ali Yadollahpour¹, Mansour Zabihzadeh^1,2* and FoadGoli Ahmadabad³

¹Department of Medical Physics, School of Medicine, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. ²Department of Radiation Oncology, Golestan Hospital, Ahvaz, Jundishapur University of Medical Sciences, Ahvaz, Iran. ³Department of Medical Physics, School of Medicine, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran.

DOI : https://dx.doi.org/10.13005/bpj/396

Abstract

Determining dose distribution around the brachytherapy sources is crucial to establish an accurate treatment planning. In this study dosimetric parameters of 252CF as neutron brachytherapy source were calculated using Monte Carlo simulation method.Physical and geometrical parameters of 252CF source were simulated by MCNPX (2.6.0)modeling code. Air kerma strength, Sk, of source positioned inside a vacuum sphere was calculated. Recommended dosimetric parameters by AAPM, TG-43 protocol were calculated by centering source in a homogeneity phantom.The air kerma strength of 252CF source was estimated 0.345 (cGycm2/¼gh). Dose rate constant was 7.014 cGyh-1U-1. The Radial dose function with 5 degree equation was estimated by gN(r) = 1.1745+0.2298r+0.061r2+-0.0109r3+0.0009r4+-3E10-5r5. Numerical amounts of the anisotropy dose functions and the related equations were calculated.Despite low-energy emission photons and high dose gradients with radial distance, dosimetric parameters of the model 6711 I-125 source can be calculated by MCNPX Monte Carlo code with acceptable accuracy. Calculated parameters of the model 6711 I-125 brachytherapy source can be used by treatment planning systems for brachytherapy.

Keywords

Brachytherapy; Neutron dosimetry; 252CF Source; Monte Carlo Simulation

Download this article as: 

Copy the following to cite this article: Yadollahpour A, Zabihzadeh M, Ahmadabad F. Calculation of Dose Distribution Around a Clinical 252Cf Source for Neutron Therapy Based on AAPM, TG-43 Protocol. Biomed Pharmacol J 2013;6(2)

Copy the following to cite this URL: Yadollahpour A, Zabihzadeh M, Ahmadabad F. Calculation of Dose Distribution Around a Clinical 252Cf Source for Neutron Therapy Based on AAPM, TG-43 Protocol. Biomed Pharmacol J 2013;6(2). Available from: http://biomedpharmajournal.org/?p=2657

Introduction

Compared with photon and electron beams, fast neutrons have high therapeutic ratio for tumor cells treatment. This can be attributed to the relative high biological effect, high radiation weighting factor, low oxygen enhancement ratio and high linear energy transfer of neutrons and fission fragments (1, 2). Delivering maximum and minimum dose respectively to the tumor and healthy surrounding tissues is possible through Boron Neutron Capture Therapy (BNCT) by adjusting fast neutrons before the depth of the tumor and also targeting tumor with boron element (due to the high cross section, 3837 Barn, in the reaction with thermal neutrons) (3). Despite the potential and high accuracy of BNCT method in treating various tumors, especially hypoxic tumors and advanced cancers (particularly brain tumors), high costs and the need for reactors to produce a neutron beam, has limited the widespread use of this technique (4).

Accordingly, the use of radioisotopecalifornium-252 (²⁵²CF) as neutron emitter is proposed recently in radiation treatment, based on Neutron Brachytherapy (NBT) as a cost effective treatment method (5). Using ²⁵²CF in radiation therapy was introduced for the first time by Schlea and Stoddard (6). The half-life of ²⁵²CF is approximately 2.645 years and in 96.6% cases decays with alpha particles irradiation and 3.1% of the disintegration will lead to nuclear fission. In each fission, on average, 3.768 neutrons are released; 1 gram ²⁵²CF, irradiates 2.314×10⁶ neutrons per second, with a most probable energy in 0.7 MeV (The neutron energy spectrum follows the Watt function, from 1eV to 20MeV) (7) which provide appropriate flux for brachytherapy (4, 8).

Performing neutron brachytherapy accurately and achieving the maximum tumor dose and the minimum dose of normal tissues require appropriate determination of dose distribution around the ²⁵²CF source; the results will be subsequently used in the treatment designing software. In the present study, dosimetry parameters of ²⁵²CF source is calculated using Monte Carlo calculations and based on the proposed protocol AAPM-TG ​​43 (9).

Materials and Methods

Simulation code MCNPX (2.6.0) (8) was used for the simulation calculations. The energy of neutron cutoff was considered equal to 0.1 eV. No method was applied to reduce the error of neutron transport in the programs. The neutron scattering cross sections in the solid state, S (a, b), named lwtr.01t, was used in order to precisely calculate the transport of slow neutrons from the cross sections of thermal neutrons. In the simulation programs of this study, the number of transported neutron from neutron source was considered equal to 10⁸ resulting in less than 5% error in the farthest distance from the source (11 cm).

CF Neutron Source

The dimensions and materials of ²⁵²CF neutron source utilized in this study are shown in Figure 1. The active element of cylindrical source is made ​​of californium oxide, Cf₂O₃, with 12 gr/cm³ density. The cylinder height and radius is 1.5 and 0.615 cm respectively, which is located in a platinum – iridium 10% capsule (Pt/Ir-10%), with following characteristics: density= 21.55 gr/cm³, the inner diameter= 0.135 cm, the external diameter= 0.175 cm, internal length= 1.55 cm and the external length= 1.77 cm. The internal and external diameter and the internal and external length of the outer capsule is 0.18, 0.28, 1.782 and 2.314 cm, respectively. As a part of the design, a spherical eye let with the diameter of 0.0635 cm is embedded at the end of the source. ²⁵²CF fission energy spectrum is considered as a function of W (4, 8), with the following equation:

 

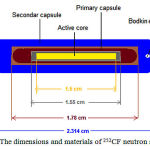Figure 1: The dimensions and materials of 252CF neutron source   Click here to View figure

Protocols AAPM-TG.43 and Neutron Source Dosimetry of ²⁵²CF

Based on the proposed protocol AAPM-TG ​​43 (9), the absorbed dose rate of ²⁵²CF neutron source is calculated anywhere around the source. This computing is performed in the water phantom, , in terms of the radial distance from the central source, r, and the angle from the central axis of the source, q,  and with the following equation:

 

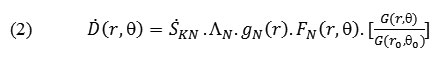
Where,S_KN , the air kerma strength in a vacuum environment is the product of air kerma rate and the square of the distance from the source center:

Λ_N, the constant of neutron dose rate is calculated by dividing the source neutron dose rate (in terms of cGy/μgh in the perpendicular axis reference point on the central axis of the source),0_° =90°, r_{0 ^{= cm,}} in a homogeneous water phantom by air kerma strength,S_KN :

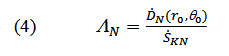
Neutron absorbed dose is calculated positioning the source in the center of the water phantom with the dimensions 30×30×30cm³ (using *f8 tally on perpendicular-axis to the central axis, 1 cm, and the sphere voxel with the radius of 0.5 cm) and is divided by the air kerma strength. The calculated simulation outputs are converted to Gy absorbed dose unit applying relevant coefficients.

The radial dose function, g_N(r), considers the dependence of neutron absorption and photons scattering along the transverse axis in the medium and is expressed as follows:

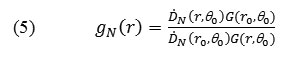
According to the practical calculations, the best equation to express the radial dose function is the fifth grade function:

The radial dose function, g_N(r), is calculated by *f8 tally in the cylindrical shell around the central axis of the source, with 0.4cm thickness, at a distance of 0.2cm to 11cm from the source center and is converted to dose rate applying appropriate coefficients.

G (r, θ) is a geometric factor that considers the reduction of the neutrons flow, at any distance from the source and based on the geometry of the source; this is dependent on the distribution of radioactive material in the source. Considering the point source, G (r, θ) = 1/r² applies and for a line source with uniform distribution of geometric factor the equation is:

Where L is the length of the source active element. For example, for θ = 90, the geometric factor to calculate the radial dose function is expressed as follows:

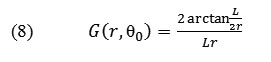
In this study, the more stringent assumption of source linearity has been used and these coefficients were calculated separately for the studied points in the radial distances and at different angles.

Anisotropy function, F_N(r, θ), takes into account non-homogeneity , angular dependence of neutron absorption and scattering within the source capsule and is expressed in the Eq. (8) as follows: (10):

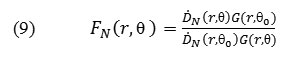
Anisotropy function, F_N(r, θ), was calculated using Eq. 8 at intervals of 2, 3, 5, 8, 10 cm and at angles of 0, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90 degrees in a water phantom.

Results

Air Kerma Rate and Dose Rate Constants

Air kerma strength of neutrons, , is calculated and with a 3% error is equal to 0.345 (cGy cm2/μgh) or 0.345 U/μg. Dose absorbed rate in water at a distance of 1cm from the source center,D_N(r₀,0₀) , is 2.075 cGy/μgh; the constant of neutron dose rate, Λ_N, was estimated 6.014 cGy/Uh, dividing dose absorbed rate by the air kerma strength of the neutrons in the air.

Radial Dose Function

The calculated values ​​for the radial dose function, g_N(r), are presented in Table 1. The resulted coefficients from 5 fitted variables on the values of radial dose function based on the radial distance, r, is obtained as follows:

A₀=1.17545, a₁=-0.2298, a₂=0.061, a₃=-0.1090, a₄=0.9000, a₅=-3×10^-5

Table 1. The calculated values ​​of the radial dose function, g_N (r), based on the radial distance, r, from the source center of ²⁵²CF.

radial dose function, gN(r)	Distance from the source center (4)	radial dose function, gN(r)	Distance from the source center (4)	radial dose function, gN(r)	Distance from the source center (4)
0.548	7	0.755	3.8	1.050	0.6
0.536	7.2	0.742	4	1.030	0.8
0.524	7.4	0.728	4.2	1.000	1
0.513	7.6	0.716	4.4	0.975	1.2
0.501	7.8	0.712	4.6	0.449	1.4
0.490	8	0.689	4.8	0.920	1.6
0.478	8.2	0.764	5	0.900	1.8
0.467	8.4	0.662	5.2	0.882	2
0.457	8.6	0.648	5.4	0.867	2.2
0.447	8.8	0.634	5.6	0.852	2.4
0.438	9	0.622	5.8	0.837	2.6
0.427	9.2	0.610	6	0.824	2.8
0.418	9.4	0.597	6.2	0.810	3
0.409	9.6	0.584	6.4	0.796	3.2
0.399	9.8	0.571	6.6	0.782	3.4
0.389	10	0.560	6.8	0.769	3.6

Anisotropy Dose Function, F_N(r, θ)

The obtained values for dose anisotropy function, F_N(r, θ) are shown in Table 2. As expected,                                 increasing the radial distance and angle to the source central axis leads to enhancing the calculated values ​​for the anisotropy dose.

Table 2. The calculated values for dose anisotropy function, F_N(r, θ)

Angle to the central axis of the 252CF (degree)											Radial distance (4)
90	80	70	60	50	40	30	20	10	2	0
1.001	1.010	0.999	0.999	0.989	0.987	0.974	0.960	0.960	0.943	0.92	2
1.008	1.101	0.998	0.999	0.989	0.988	0.977	0.970	0.97	0.954	0.93	3
1.007	0.988	1.023	1.004	0.994	0.989	0.983	0.987	0.95	0.97	0.95	4
1.008	0.998	1.020	1.01	0.995	0.995	0.985	0.988	0.94	0.987	0.967	5
1.001	0.989	1.004	1.008	0.996	0.997	0.984	0.991	0.96	0.989	0.998	8
0.999	1.001	1.008	1.070	0.998	0.999	0.988	0.999	0.986	0.99	1.01	10

Discussion

In all discussed studies at following, dose calculations and measurements were reported based on protocols AAPM, TG-43 (7) and the length of source’s active element was equal to 1.5 cm. The computed air kerma strength for ²⁵²CF,D_N(r₀,0₀) , is equal to 0.3450 (cGy cm2/μgh) or 0.3450 U/μg which is consent with other reported results, 0.3348, 0.3350, 0.3300 cm2/ μgh, respectively by Ghassoun et al. (11), Paredes et al. (12) and Rivard et al. (4). The calculated absorbed dose rate in the water phantom, at a distance of 1cm from the source center on the central axis and perpendicular to the central axis of ²⁵²CF,D_N(r₀,0₀) , are compared to other results (Table 3) (3, 4, 11-15). The minimum calculated difference of D_N(r₀,0₀)  is -0.86% with the measured data of Colvett et al. (14) and the greatest difference was found to be +11.81% with Ghassoun et al. (11).

Table 3. The calculated absorbed dose in water phantom, , at distance of 1cm from the source center on the central axis and perpendicular to the central axis of the ²⁵²CF source.

Absorbed dose rate (cGy / μgh) in water, , at a distance of 1cm from the source center
1.929	Krishnaswamy (13)
2.093	Colvett et al. (14)
1.900	Yanch and Zamenhof (3)
1.880	Wierzbicki et al. (15)
1.873	Rivard et al. (4)
1.916	Paredes et al. (12)
1.868	Ghassoun (11)
2.075	Current Research

The constant of dose rate in ²⁵²CF source, Λ_N, are compared in Table 4 with the previous results. The calculated constant of dose rate in ²⁵²CF source, Λ_N, is equal to 6.014 cGy/Uh and was consistent (+5.95%) with 5.676 cGy/Uh, reported by Rivard et al. (4). Since the constant of neutron dose rate depends on the geometry of the source and the adsorbent environment, the constant of dose rate might change due to the geometrical characteristics, the source capsule material, phantom material, or on the clinical basis the tissue material the source has been planted in (4, 11, 12).

Table 4. The constant of dose rate in ²⁵²CF source, Λ_N, in comparison with other results reported.

The constant of dose rate, ΛN, 252CF source (cGy/Uh)
5.676	Rivard et al. (4)
5.579	Ghassoun (11)
5.719	Paredes et al. (12)
6.014	Current Research

Among the reviewed studies only Colvett et al. (14) is based on the measurement; Colvett’s dose radial function is reported to a depth of 6 cm and is in good agreement with the results of the present study (14). The cross section of the neutrons interaction with material highly depends on the weights of the elements (especially hydrogen content), the density of the target material and also the neutron spectrum used.

The unacceptable differences between the constant of dose rate and anisotropy functions reported in Wierzbicki et al. (15) compared to the present and other studies is mainly due to the difference in the source radiation neutron spectrum, hydrogen content and water density as the corresponding tissue. For example, Krishnaswamy (13) considered the watt energy spectrum for the ²⁵²CF source, a=0.9756 and b=2.926, which is 0.88 and 2 in this study. On the other hand, for example in the Colvett et al. (14) and Krishnaswamy (13) studies absorbed dose is considered in tissue-equivalent material instead of water in which densities are 1.06 and 1.00 g/cm³ respectively, containing 10.3% and 10.5% hydrogen. Wierzbicki et al. (15) and Yanch and Zamenhof (3) used water phantom with density of 1.00g/cm³, containing 11.2% hydrogen.

Another reason for these discrepancies is probably taking into account different values for the neutron source flux. For example, the neutron flux considered in this study is equal to 2.314×10⁶ n/μgs, while Colvett et al. (14) used the flux of 2.339×10⁶ n/μgs. Based on these results appropriate correction factors must be applied to make different factors equivalent such as the energy spectrum, different materials in report environment, absorbed dose and neutron flux.

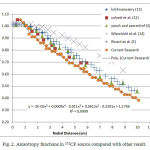Figure 2: Anisotropy functions in 252CF source compared with other result.   Click here to View figure

Conclusion

The present study calculated dosimetry parameters of ²⁵²CF source as recommended by AAPM, TG-43 (9) for implementing Monte Carlo simulation ( MCNPX) (16). Air kerma strength computed for ²⁵²CF source, , is equal to 0.3450 U/μg, absorbed dose rate in water at a distance of 1cm from the source center,  is 2.075 cGy/μgh and the constant of dose rate, Λ_N, is 6.014 cGy/Uh; these calculated data are in good agreement with simulation studies and measurements have been reported . The calculated values are operative​​ with a high confidence in brachytherapy software designing and numerical calculations in brachytherapy units with a ²⁵²CF source.

Acknowledgment

This study was performed as a part of a Master thesis at the Department of Medical Physics, Ahvaz Jundishahpur University of Medical Sciences and was financially supported by the research project No. u=92043u.

 References

1. Maruyama Y. Californium-252 : New radioisotope for human cancer therapy Endocurietherapy/Hyperthermia Oncology. 1986(2):171-87.
2. Russell KJ, Caplan RJ, Laramore GE, Burnison CM, Maor MH, Taylor ME, et al. Photon versus fast neutron external beam radiotherapy in the treatment of locally advanced prostate cancer: results of a randomized prospective trial. International Journal of Radiation Oncology* Biology* Physics. 1994;28(1):47-54.
3. Yanch J, Zamenhof R. Dosimetry of 252Cf sources for neutron radiotherapy with and without augmentation by boron neutron capture therapy. Radiation research. 1992;131(3):249-56.
4. Rivard MJ, Wierzbicki JG, Van den Heuvel F, Martin RC, McMahon RR. Clinical brachytherapy with neutron emitting Cf sources and adherence to AAPM TG-43 dosimetry protocol. Medical physics. 1999(26):87-96.
5. Blasko JC, Ragde H, Luse RW, Sylvester JE, Cavanagh W, Grimm PD. Should brachytherapy be considered a therapeutic option in localized prostate cancer? Urologic Clinics of North America. 1996;23(4):633-50.
6. Schlea CS, Stoddard DH. Californium isotopes proposed for intracavity and interstitial radiation therapy with neutrons. Nature (Londan). 1965(206):1058-9.
7. Caswell RS, Coyne JJ, Randolph ML. Kerma factors of elements and compounds for neutron energies below 30 MeV. Applied Radiation and Isotopes. 1982;33(11):1227-62.
8. Mannhart W. Evaluation of the Cf-252 fission neutron spectrum between 0 and 20 MeV. IAEA-TECDOC. 1987(410):158-71.
9. Rivard MJ, Coursey B. M., DeWerd LA, Hanson WF, Huq MS, Ibbott GS. Update of AAPM Task Group No. 43 Report: A revised AAPM protocol for brachytherapy dose calculations. Med Phys. 2004;31 „(3):633-74.
10. Ghassoun J, Chkillou B, Jehouani A. Spatial and spectral characteristics of a compact system neutron beam designed for BNCT facility. Appl Radiat Isot. 2009;67(4):560-4.
11. Ghassoun J, Mostacci D, Molinari V, Jehouani A. Detailed dose distribution prediction of Cf-252 brachytherapy source with boron loading dose enhancement. Applied Radiation and Isotopes. 2010;68(2):265-70.
12. Paredes L. Neutrons absorbed dose rate calculations for interstitial brachytherapy with 252Cf sources. NIMA. 2007(580):582–5.
13. Krishnaswamy V. Calculated depth dose tables for californium-252 sources in tissue. Physics in Medicine and Biology. 1972;17(1):56-63.
14. Colvett RD, Rossi HH, Krishnaswamy V. Dose distributions around a californium-252 needle. Physics in Medicine and Biology. 1972;17(3):356-64.
15. Wierzbicki JG, Rivard MJ, Roberts W. Physics and dosimetry of clinical 252 Cf sources in Ref. 1997;29:25-53.
16. Walter LS. (Ed.). LANL (Los Alamos National Laboratory) Monte Carlo N-Particle transport code system for multiparticle and high energy applications. Version 240, LA-CP-02-408, Los Alamos National Laboratory. 2002.