Manuscript accepted on :December 12, 2016
Published online on: --
Plagiarism Check: Yes
Udayakumar E, Santhi S, Gowrishankar R, Shivkumar S and Sathish Kumar G
Department of ECE, KIT-Kalaignarkarunanidhi Institute of Technology, Coimbatore, Tamilnadu, India.
Corresponding Author E-mail: udayakumar.sujith@gmail.comDOI : https://dx.doi.org/10.13005/bpj/1188
Abstract
This paper proposed an automated reconstruction of cortical surfaces using T1-weighted magnetic resonance images. A unified reeb analysis frame work has been used for the detection and removal of geometric and topological outliers on tissue boundaries. The system can pin point the position of spurious branches and topological outliers using intrinsic reed analysis. It is also used to rectify the tissue with confined filtering using information from both image intensity distributions and geometric regularity. For enhanced heftiness to image in homogeneity, and adaptive interpolation to attain sub-voxel accuracy in rebuilt surfaces, an enhanced tissue arrangement with Hessian features was developed using this system. A new system was designed by integrating these novel developments. The cortical surfaces with enhanced quality and vividly reduced computational cost when compared with the popular free surfer software can be automatically reconstructed using this system. The surfaces that well represent cortical anatomy and create thickness features with higher statistical power in population studies is shown in the presented work by comparing with free surfer.
Keywords
CT; MRI; CSF GM; LB; Reeb; Sulcal; and
Download this article as:| Copy the following to cite this article: Udayakumar E, Santhi S, Gowrishankar R, Shivkumar S, Kumar S. G. An Unified Reeb Analysis for Cortical Surface Reconstruction of Mri Images. Biomed Pharmacol J 2017;10(2). |
| Copy the following to cite this URL: Udayakumar E, Santhi S, Gowrishankar R, Shivkumar S, Kumar S. G. An Unified Reeb Analysis for Cortical Surface Reconstruction of Mri Images. Biomed Pharmacol J 2017;10(2). Available from: http://biomedpharmajournal.org/?p=14787 |
Introduction
A critical problem in brain mapping of MRI images, where reconstructing cortical surface which is for measuring tissue integrity and morphometry. For improving the speed, robustness and accuracy of cortical reconstruction lot of algorithms were developed. The T1-weighted MR images1 of automated reconstruction of cortical surfaces using Laplace Beltramic(LB) eigen function based on analysis of topology and geometry were analysed. A many number of data set of high quality cortical surfaces can be reconstructed. A set of standard scans is a T1-weighted scans and finds the spin-lattice, T1 relaxation time in tissues of our body. It has gradient echo or spin echo sequences and RF pulse is increased for T1-weighted contrast.
The objective is to diagnose the MRI Images of automated reconstruction of cortical surfaces of geometrical and topological outliers. MRI produces the high quality 2D/3D images of human anatomic tissues by using the interaction of protons with strong external magnetic field and Radio frequency. It is superior to other imaging techniques, such as computerized Tomography (CT), ultrasound and X-Ray in the area of clinical diagnosis of human brain. Reconstruction in MR images is challenging due to intensity homogeneity, low intensity contrast among adjacent Grey Matter (GM) structures, structure topological variation among people, and random noise. Intensity inhomogeneity is unavoidable in MR brain images,2 this intensity inhomogeneity can be more than 30% variations of image intensity for the same brain tissue, and it is even more severe in the high field MR images. Another difficulty is the low intensity contrast which makes the boundaries between the adjacent GM structures blurry and in some cases even invisible.
System Design
The T1-weighted MR Images of automated cortical reconstruction was developed.6 For this the WM and GM surface was reconstruct and for such surfaces, the Surface evolution algorithm was used. The LB eigen function was computed and tissue boundaries of manifold system was represented and build. For correcting and detecting the topological and geometrical outliers3 a unified approach was developed. The intrinsic reeb analysis to perform filtering without shrinkage for geometric outliers was intended. The Flow diagram is shown in Fig. 1.
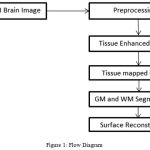 |
Figure 1: Flow Diagram
|
Preprocessing
For the input image the Gaussian filtering was used to remove the noise, where wiener2 function is used. One of the windowed filter is the Gaussian filter is mean weighted. According to Gaussian distribution, the weights in the filter was calculated.
Tissue Enhanced Image
Based on the hessian matrix we can identify the tissue enhanced image. Hessian is a square matrix of second order of a partial function. The local curvature of a function of many variables can be described.
Tissue Mapped Image
For an average atlas building, group wise implementation is used. For brain MRI registration the free-surfer segmentation was used. For traced structures reduction of morphological results and variance was compared against traditional MRI based segmentation. The correction using RFT for MRI and multi structure registration was used.
GM and WM Segmentation
The cortical grey matter is converted as volumetric representation by label values from the surface. The cortical surface based cortical folding patterns was mapped by the surface based labels.
The Grey matter mask was subjected to average space to transform as grey matter segmentation.12 The multi structure registration was average generated while cortical folding patterns was greater one.
Surface Reconstruction
Geometrical topology is a numerical technique for tracking interfaces and shapes. The advantage of the level set method is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects, bounded region with a well-behaved boundary.
Results and Discussion
The cortical surfaces reconstruction of requires the image analysis system that includes preprocessing steps such as nonlinear registration, inhomogeneity correction, and tissue classification and skull stripping. The MRI Synthetic Input Images 1 is shown in Fig. 2.Where the GUI for cortical surface reconstruction is shown in Fig. 3.
MRI Synthetic Input Images
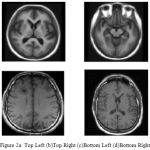 |
Figure 2a: Top Left (b)Top Right (c)Bottom Left (d)Bottom Right
|
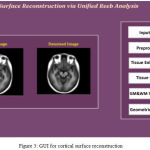 |
Figure 3: GUI for cortical surface reconstruction
|
Many of preprocessing methods are located a well known smooth white matter surface, which represents the boundary between WM and gray matter, with good topology is first reconstructed6 and then deformed to find the GM surface that includes the boundary of the cerebrospinal fluid and GM. The GM and WM Segmented image 1 is shown in Fig. 4. The Tissue Mapping and Tissue Segmented of input Image 1 in shown in Fig. 5 and Fig. 6.
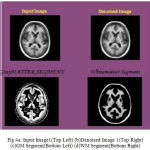 |
Figure 4a: Input Image1(Top Left) (b)Denoised Image 1(Top Right) (c)GM Segment(Bottom Left) (d)WM Segment(Bottom Right)
|
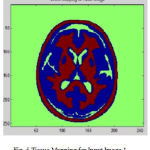 |
Figure 5: Tissue Mapping for Input Image 1
|
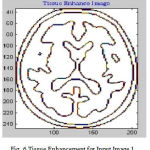 |
Figure 6: Tissue Enhancement for Input Image 1
|
During the reconstruction of surface process topological outliers and geometrical outlines occurs frequently due to half failure of preprocessing steps, anatomical population and image resolution. Both types of outlines is removed without accuracy and they were repeated in past work in order to produce high quality tissue boundary. The GM and WM Segmented image 2 is shown in Fig. 7. The Tissue Mapping and Tissue Segmented of input Image 2 in shown in Fig. 8 and Fig. 9.
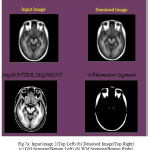 |
Figure 7a: Input image 2(Top Left) (b) Denoised Image(Top Right) (c) GM Segment(Bottom Left) (d) WM Segment(Bottom Right)
|
The geometric out-layers was avoided for smoothness regularization. This regularization based method has two problems. The non-removal of skull stripping due to leakage into areas of non-cortical surfaces where the geometric outliers occurrence may be form or else. The sulcal region shrinkage can arise due to regularization. The GM and WM Segmented image 3 is shown in Fig. 10.
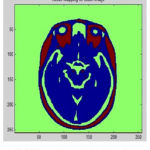 |
Figure 8: Tissue Mapping for Input Image 2
|
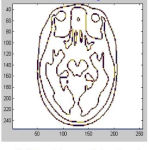 |
Figure 9: Tissue Enhancement for Input Image 2
|
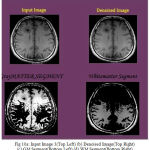 |
Figure 10a: Input Image 3(Top Left) (b) Denoised Image(Top Right) (c) GM Segment(Bottom Left) (d) WM Segment(Bottom Right)
|
In cortical thickness measurement, 38 accuracy is affected and leads to decreased power in statistical analysis. The topological analysis and graph analysis is due to geometric size of voxel space is formed. The Tissue Mapping and Tissue Segmented of input Image 3 in shown in Fig. 11 and Fig. 12.
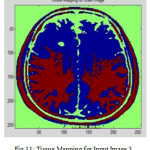 |
Figure 11: Tissue Mapping for Input Image 3
|
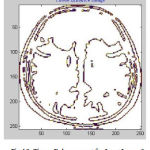 |
Figure 12: Tissue Enhancement for Input Image 3
|
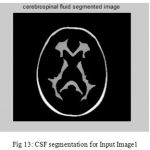 |
Figure 13: CSF segmentation for Input Image1
|
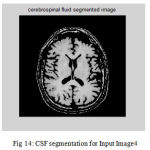 |
Figure 14: CSF segmentation for Input Image4
|
The second step is the mesh representation of the triangular surface and detects the topological outlier from overlapping triangular after mapping surface to the sphere. The fill decisions are made according to curvature distribution and image intensity. The CSF and CSF Segmented of input Image 1 and 3 in shown in Fig. 13 and Fig. 14.The disadvantage of this method are not suitable for complicated surfaces and for outlier detection. The main thing of the system is a unified approach based on intrinsic geometry for the correction of topological and geometric outliers. Where the Geometrical topology processed output for input image 4 and 1 is shown in Fig. 15 and Fig. 16.
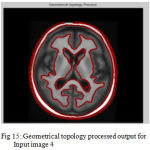 |
Figure 15: Geometrical topology processed output for Input image 4
|
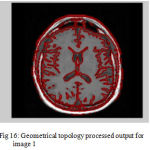 |
Figure 16: Geometrical topology processed output for image 1
|
Conclusion
This technique has developed for automatic cortical reconstruction from T1-weighted MR images. It is demonstrated that the system is used to create high quality surface with much low computational cost when compared with free surfer. The unified technique proposed in thus work for the determination of geometric and topological structures, is normal and acceptable for other medical image determination problems. Thus work is intensive on the reconstruction of the WM and GM surfaces. There is a considerable interest available for attaining a central cortical surface from MR images is same as an equal representation of the WM and GM surfaces. To achieve this goal two different techniques are followed. By using evolution algorithm should be created to evolve the WM surface to the center of the GM tissue. Shape analysis technique is used to determine the central cortical surface. This technique established an intrinsic surface mapping method that can construct WM and GM surfaces towards one another in a huge dimensional embedding space from optimizing their conformal metrics. By introducing one-to-one correspondences between two surfaces with this intrinsic mapping algorithm, This work can obtain the central cortical surface as the mean shape of two surfaces. Using the one to one map between the surfaces, enhanced a very strong method to obtain cortical thickness in the most case of neighboring sulcal banks with highly unequal thickness.
References
- Udayakumar E.,Sree R. A., Srihari K., Rajesh S and Vaishnavi R. Certain Investigation on Pathologies in Brain Images using MRI Slicing, Middle-East Journal of Scientific Research, IDOSI Publications. 2015;6:1076-1084.
- Udayakumar E., Santhi S., Gowrishankar R.,Ramesh C., Gowthaman T. Region Growing Image Segmentation for Newborn Brain MRI. BioTechnology: An Indian Journal, Trade Science Inc Journals. 2016;12(12):1-8.
- Carman G. J., Drury H. A and. Van Essen D. C. Computational methods for reconstructing and unfolding the cerebral cortex. 1995.
- Xu y. C., Pham L. D.,Rettmann E. M. Reconstuction of the Human Cerebral Cortex from MR Images, IEEE Transaction on Medical Imaging. 2009.
- Cohen. Quantitative methods in psychology: A power primer, Psy-chol. Bull. 1992;112(1):155–59.
- Dale A. M., Fischl B and Sereno I. M. Cortical surface-based analysis I: Segmentation and surface reconstruction. NeuroI-mage. 1999;9:179–194.
CrossRef - Dinovetal I. Efficient, distributed and interactive neuroimaging data analysis using the LONI Pipeline,Front. Neuro inform. 2009.
- Pont D and Plummer. Power and sample size calculations: A review and computer program,Control. Clin .Trials. 1990;11:116–28.
CrossRef - Grant p. E.,Qi Y., Han X. Cortical Surface Shape Analysis Based on Spherical Wavelets, IEEE Transactions on Medical Imaging. 2007.
- Segonee F.,Pacheco J and Fischl B. Geometrically Accurate Topology-Correction of Cortical Surface using Non seperating Loops. 2001.
- Han et al. CRUISE: Cortical reconstruction using implicit surface evolution. Neuro-Image. 2004;23:997–1012.
CrossRef - Hinshaw P. K., Poliakov V. A., Moore Shape Based Cortical Surface Segmentation for Visualization Brain Mapping. 2001.
- Kim J. S et al., Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. Neuro-Image. 2005;27:210–221.
CrossRef - MacDonald D. A method for identifying geometrically simple surfaces from three dimensional images, Ph.D. dissertation, McGill Univ., Montreal, Canada. 1998.
- Mangin et al From 3D magnetic resonance images to structural representations of the cortex topography using topology preserving deformations. J. Math. Imag. Vis. 1995;5(4):297–318.
CrossRef - Miller M. I., Massie A. B., Ratnanather J., Botteron K. N and sernansky. Bayesian construction of geometrically based cortical thickness metrics. Neuro Image. 2000;12(6):676–687.







