Hamed Ameri^1*, Ali Esteki², Ahmad Ameri³

¹Department of  Biomedical Engineering , Science and Research Branch, Islamic Azad university,Tehran, Iran ²Department of Biomedical Engineering and physics, shahid beheshti university of medical sciences, Tehran, Iran ³Department of Ophtalmology,School of Medicine , Tehran University of Medical Sciences, Tehran, Iran  

DOI : https://dx.doi.org/10.13005/bpj/834

Abstract

Many patients come afoul by the over correction or under correction of the eye muscles after strabismus surgery. This is related to the individual properties of anyone’s distinct eye muscles. Therefore it is necessary to have accurate information about the living soft tissues in simulations and the proper modeling of the human eye muscles. In vivo properties of the eye muscles have not been explored sufficiently. There are many problems in experimental works such as a lack of a standard methodology and disagreements between model and experimental data. The aim of this work is to exhibit an in vivo measurement in strabismus surgery to study the viscoelastic properties of the horizontal eye muscles and present a three element model which consists of a spring in parallel with a Maxwell element which was composed of a dashpot and a spring in series. The test was performed on 2 women and 5 men under general anesthesia.Three different loads (10, 15, and 20 grams) were applied onto the medial rectus over a maximum time period of up to 10 seconds. The response of the linear and nonlinear three element model was fitted to the obtained creep graphs. The results showed a good fitness in both the linear and non-linear model. Since the living soft tissues generally exhibit nonlinear behavior, these results can indicate that the experiment have done in linear range.It would be useful to predict any patient’s eye muscle performance after strabismus surgery.  

Keywords

strabismus; medial rectus; in vivo measurement

Download this article as: 

Copy the following to cite this article: Ameri H, Esteki A, Ameri A. An in Vivo Creep Test and Mechanical Modeling in Strabismus. Biomed Pharmacol J 2015;8(2)

Copy the following to cite this URL: Ameri H, Esteki A, Ameri A. An in Vivo Creep Test and Mechanical Modeling in Strabismus. Biomed Pharmacol J 2015;8(2). Available from: http://biomedpharmajournal.org/?p=3057

Introduction

Any type of deviation from a correct alignment of the eye is known as strabismus. It is imperative to have accurate information about the passive and active eye muscles and their corresponding lengths. In order to orient the eye in a certain position, such information aids the surgeon in adopting a suitable approach as to how much of the ocular muscle must be resected or recessed. As of now, many standard tables[i] which have been acquired experimentally and statistically are being used to correct eye deviation; nevertheless, some patients come afoul by the over correction or under correction[ii] as a result of this operation. One of the most important reasons for this is related to the individual human body properties. The adjustable suture method[iii] is one solution to this problem, but the patient has to be controlled by the surgeon in order to acquire the suitable length for patient’s eye muscles. The human body has various types of muscles, therefore understanding the muscle properties and modeling and characterizing the mechanical response of them, is one of the important problems in biomechanics. The mechanical behavior of living soft tissue is affected by their structure, including microscopic morphology, chemical composition. Therefore, the in vitro behavior of living soft tissues may not sufficiently describe in vivo behavior. One of the main problems in studying living soft tissue is the lack of standard methodology for in vivo experimental studies. Tissues usually exhibit nonlinear viscoelastic properties. The viscoelastic models are shown in different types and has been extensively discussed in material science. One type of such model is the multi-component model that is composed of one or many spring(s) and dashpot(s) in different arrangement. The purpose of this work is to design a device to test eye muscle tissues in vivo and present a simple model to describe creep behavior of the horizontal eye muscles.

Materials and Methods

Components of the device

A test device (fig. 1 )was designed in order to find the linear and nonlinear viscoelastic properties of the eye muscles. It was composed of an adjustable support, a connection rod, an optical encoder, a pulley system that is related to the globe with a traction suture, and a set of weights ranging from 10-20 grams.

Functions of the device

The test device used in this study was designed to exert a constant force to the horizontal eye muscles of patients undergoing strabismus surgery. The support of the device was installed beside the patient’s bed close, the patient’s head. The connecting rod angle was adjusted so that the pulley was placed along the eyeball. A suture thread was connected at the 6 and 12 o’clock positions of the cornea to move the eyeball and the rest of the thread was twisted around the pulley shaft, while avoiding slippage of the thread. The weights were hung along the rest of thread. Three standard weights of 10, 15, and 20 grams were used to apply a constant force.

Optical encoder

To measure the amount of eye muscle movement , a HEDS-9700 series optical encoder with a two channel output from the encoder was used. The output data was received by the sound card of the laptop.

Dial gauge

To measure the displacement in analog method , a dial gauge was used where the axis of rotation of it’s pulley and shaft were the same. Therefore any rotation of the pulley could be shown. The movement of the pointer was recorded by a Canon video camera during the time.

Software and hardware of the data acquisition

The elongation of eye muscle was recorded in real time at a 44100 kHz data collection rate onto a core i7 laptop hard disk. A program written in LabVIEW was used in data acquisition from an optical encoder. A MATLAB program was used for the analysis and de noising of the recorded data. The movement of the dial gauge pointer was recorded by a Canon camera at the time of data acquisition.

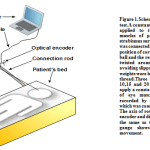Figure 1: Schematic  of in vivo creep test.A constant force (weight) was applied to the horizontal eye muscles of patients undergoing strabismus surgery Click here to view full figure

 

Determination of mechanical properties of the thread

Since the test might be affected by mechanical properties of the suture thread, the suture thread was tested with 10, 15, and 20 grams loads for a duration of 60 seconds. It was found that no time dependent behavior was demonstrated.

Selected patients

The selected patients consisted of five men ages 24, 10, 39, 20, and 13 years old and two women ages 20 and 31. All became afoul by esotropia or exotropia.

Surgery method

The patients were anesthetized in stage 3 by the drug Propofol under anesthesiologist control.

Creep test

When subjected to a constant force, viscoelastic materials experience a time dependent increase in deformation(length). This phenomenon is known as viscoelastic creep.The creep test was applied to the medial rectus of 7 strabismic eyes(5 men and 2 women) by using 10, 15, and 20 gram static forces under general anesthesia. A 60 second rest period was given between the test avoiding recovery interference. The weight was fixed by the surgeon and then suddenly released.

Viscoelastic model of eye muscle

The mechanical behavior of biological soft tissues have been widely investigated[i]. The tissues exhibit viscoelastic behaviour[ii].The word viscoelastic is composed of words viscous and elastic.A viscoelastic material exhibits both viscous(fluid behavior) and elastic (solid behavior)behavior. A viscoelastic model can be made by various combinations of the elastic spring and the viscous dashpot. These are known as mechanical models. The spring is used to simulate the mechanical behavior and dashpot is used to simulate fluid behavior of materials.One of the viscoelastic models of soft tissue that has been widely employed because of it’s simplicity, is the three element model[iii]. The three element model is constructed by a spring in parallel with a Maxwell element, which consists of a spring and dashpot in series as shown infig.2.Since soft tissues generally exhibit nonlinear behavior[iv], it is reasonable to assume using a nonlinear model but both linear and nonlinear models were used in this study and their results were compared to each other. For nonlinear modeling, exponential functions that have been previously used by others[v][vi][vii] to describe the uniaxial load-deformation relations of soft tissues were used. A viscoelastic model with nonlinear parameters that has been previously proposed[viii]was used in this work as well. The constitutive equations for linear three element model are shown in equations 1 to 12.

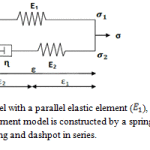Figure 2: The three element  model with a parallel elastic element (E1 ), a series elastic element (E2 ) and a dashpot (η) Click here to view full figure

 

where σ is the force, E is the elastic modulus of the material, and ε is the deformation(length) that occurs under the given force, similar to Hooke’s Law.The viscous component can be modeled as dashpots such that the force(load) – deformation rate relationship can be given as,

σ = ∫ε                                                       (6)

where  σ is the force, ∫ is the viscosity of the material, and ε  is the time derivative of deformation.

Differentiating

 

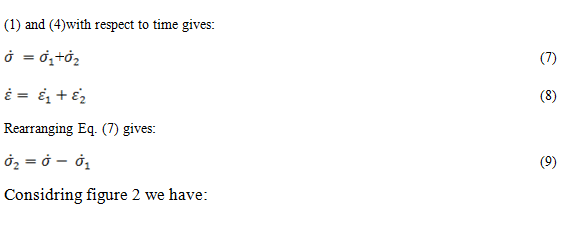
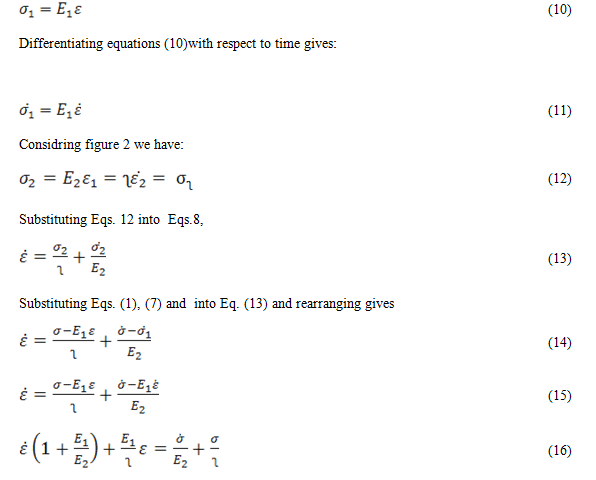
A simulink model was constructed to solve constitutive equations with linear and non-linear parameters. The input and the output of the model was force and displacement respectively.The proposed non-linear parameters that have been mentioned above are shown in equations 17 to 19.

Results

To determine the model’s parameters, the distance between the experimental data and mechanical model were minimized by using MATLAB (2012a) searching algorithm, fminsearch. This search method is iterative. The iterations continues until the Rsquared between the experimental data and the model response become closer to 1. Rsquared is the square of correlation between the experimental data and model’s response. Rsquared with a value closer to 1 shows that a greater proportion of variance is accounted by the model.Coefficients and properties of linear and nonlinear model for two patients are shown in table 1 and table 2 respectivly.Other patient’s are available upon request.A comparison between linear and nonlinear model Rsquare has been shown in table 3.

 

Table 1: Coefficients and properties of linear model for various patients
Rsquared				Model coefficients
				weight(gr)	Patient’s name
0.9899	0.00220	1.31374	0.04925	10	E.H
0.9959	0.00102	5.44425	0.019082	15
0.9807	0.00109	5.11705	0.01228	20
0.9831	0.00283	20.26104	0.018494	10	F.M
0.9930	0.00102	4.63897	0.013944	15
0.9618	0.00049	0.04446	0.010415	20

Table 1 Coefficients and properties of linear model for two patients

 

Table 2: Coefficients and properties of nonlinear model for two patients
Rsquared							Model coefficients
							weight(gr)	Patient’s name
0.9720	219.3	0.003	0.021	2.315	0.218	27.918	10	E.H
0.9815	122.92754	0.002588	0.0070567	2.65487	0.101554	98.15735	15
0.9570	84.115468	0.002059	0.0059518	2.0234	0.01905	65.99259	20
0.9780	455.327	0.0011	0.00808	2.263	0.221	62.326	10	F.M
0.9775	63.57784	0.002033	0.00588	2.32865	0.093592	62.10176	15
0.9941	125.6064	0.0040942	0.003057	3.36062	0.04352	83.20828	20

Table 2 Coefficients and properties of nonlinear model for two patients

Table 3: Comparison table of linear and non-linear model in different weights.

Non-linear model			linear model			Model type	Number
20	15	10	20	15	10	weight(gr)
Rsquared			Rsquared			Patient’s name
0.9889	0.9873	0.9869	0.9617	0.9933	0.9957	A.E	1
0.9551	0.9916	0.9936	0.9735	0.9959	0.9965	B.N	2
0.9570	0.9815	0.9720	0.9807	0.9959	0.9899	E.H	3
0.9857	0.9946	0.9857	0.9950	0.9804	0.9858	S.A	4
0.9941	0.9775	0.9780	0.9618	0.9930	0.9831	F.M	5
0.9997	0.9995	0.9972	0.8324	0.8814	0.9913	A.P	6
0.9426	0.9648	0.9714	0.9608	0.9853	0.9932	Kh.S	7

 

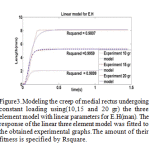Figure 3: Modeling the creep of medial rectus undergoing constant loading using(10,15 and 20 gr) the three element model with linear parameters for E.H(man). Click here to view full figure

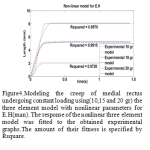Figure 4: Modeling the creep of medial rectus undergoing constant loading using(10,15 and 20 gr) the three element model with nonlinear parameters for E.H(man). Click here to view full figure

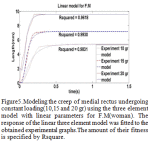Figure 5: Modeling the creep of medial rectus undergoing constant loading(10,15 and 20 gr) using the three element model with linear parameters for F.M(woman) Click here to view full figure

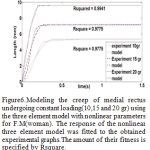Figure 6: Modeling the creep of medial rectus undergoing constant loading(10,15 and 20 gr) using the three element model with nonlinear parameters for F.M(woman) Click here to view full figure

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Discussion

The purpose of this work was designing a testing device for in vivo behavior studying and   viscoelastic properties of horizontal eye muscles in strabismus surgery. From this study we   could present a linear and nonlinear viscoelastic model of medial rectus in humans. These   models can quantify and characterize the creep of medial rectus muscles. This method is a good approach to quantify the eye muscle properties that can help physicians in strabismus surgery. However, it is not possible to characterize all of the mechanical properties of eye muscles by using this testing machine. For example to have creep recovery response it is necessary to use extra instrumentation. The study results indicated that eye muscle mechanical properties are time dependent. One of the advantages of this in vivo test method is the participation of all of the tissues that are responsible for eye movement.According to gathered creep graphs, the creep behavior of medial rectus is a nonlinear function. It was found that there were no certain patterns among each one’s creep graphs. This can be explained in terms of soft tissue, where every individual’s eye muscle properties is different. Of course the effects of the anesthesia drugs and heart rate changes must be considered during the operation. It is obvious that such factors can not be fixed during the measurement. The approach can be used for horizontal eye muscles, but it is difficult to compare this test method results directly with other methods because of different testing methodology. This work has showed that the strabismic eye muscles under tensile loads could be modeled with viscoelastic model. A three element model can show the nonlinear and linear viscoelastic behavior of the medial rectus. We tried to do the best curve fitting  for viscoelastic model with experimental data to describe the displacement as function of the time. These models can provide a criteria for evaluation of the viscoelastic properties of horizontal eye muscles and help to eliminate problems associated after strabismus operation. This work can demonstrate a relatively easy test that can characterise the steady and transient state response of medial rectus muscles. To develop this study, designing a finite element model of the medial rectus muscle would be useful. Mechanical detail of finite element model can be defined by the test results to predict eye muscles behavior.

Conclusion

The present work is a small step to specify the in vivo mechanical properties of eye muscles in    strabismus surgery. A new method and device were proposed to determine viscoelastic    properties of medial rectus muscles. It was presented as two linear and nonlinear models to    describe the creep behavior of the medial rectus. It demonstrated that both linear and nonlinear models could have a good fit on experimental data as shown in table 3. It may be indicated that we have worked in linear range of function of medial rectus. Accordingly this model can predict the creep behavior of medial rectus. We hope this study will help in more accurate strabismus  surgery.   

Acknowledgment

The author would like to thank Mr.Ebrahim Roghanizad,Mr.Hasn Hanifeh,Dr. Seyedeh Zahra Hoseininezhad,Mr.Fardin Ghavidel,Mr.Khajehoseini Mr.Ostad,Mr.Navid Resalat and Mr. Kasaee zadegan for all the help on my extraocular muscle research.

References

1. Rosenbaum AL. Santiago AP: Clinical Strabismus Management;  principles  and  surgical  techniques W.B   Saunders  company Philadelphia 1999; 435-448
2. Wilson  ME.  Pediatric  Ophthalmology  and Strabismus  .San Francisco. American Academy of  Ophthalmology 1999; 148-158
3. Ohim G. Hosohata J, Okada AA, Fujikado T, Tanohashi  N,  UchidoI.Strabismus  surgery  using  the intraoperative adjustable  suture  method  under anesthesia with propofol, Jpn J Ophthalmol. 1999; 43(6): 522-5.
4. Johson GA, Liversay GA, Woo SLY, Rajagopal KR. “A single integral finite strain viscoelastic model of ligaments and tendons,” J Biomech Eng, 1996; 118: 221-226.
5. Chimich D, Shrive N, Frank C, Marchuk L, Bray R.“Water content alters viscoelastic behaviour of the normal adolescent rabbit medial collateral ligament”, J Biomech, 1992; 25: 831-837.
6. Glantz, S.A., 1977. A three-element description for muscle with viscoelastic passiveelements. Journal of Biomechanics 10, 5–20.
7. Z. Liu and K.Yeung . The Preconditioning and Stress Relaxation of Skin TissueJournal of Biomedical & Pharmaceutical Engineering 2:1 (2008) 22-28
8. Y.C. Fung, Biomechanics: Mechanical Properties of Living Tissues, Springer, New York, 1993.
9. F. Yin, Y.C. Fung, Mechanical properties of isolated mammalian ureteral segments, American Journal of Physiology 221 (1971) 1484–1493.
10. J. Zhao, D. Liao, P. Chen, P. Kunwald, H. Gregersen, Stomach stress and strain depend on locatiion,direction and layered structure, Journal ofBiomechanics 41 (2008) 3441–3447.
11. Cheuk Wang Chung, Martin Lindsay Buist, A novel nonlinear viscoelastic solid model. Nonlinear Analysis: Real World Applications 13 (2012) 1480–1488