K.Selvakumarasamy¹, S. Poornachandra² and R. Amutha³

¹Research Scholar, Anna University, Chennai, India. ²Dean, Dept. of ECE, SNS College of Engineering, Coimbatore. India ³Professor, Dept. of ECE, SSN College of Engineering, Chennai, India.

DOI : https://dx.doi.org/10.13005/bpj/633

Abstract

  ECG is the electrical activity of the heart which uses for the various diagnostic purposes. Denoising is a process which helps to remove the noise from the original signal. Wavelet transform is suitable for non stationary signal such as ECG signal, EEG signal, PPG signal etc. The wavelet coefficients obtained by wavelet transform are made zero which in turns reduces the noise to zero level. Fuzzy logic is a structured, powerful problem solving technique that approximates a function through linguistic variables. A fuzzy membership function is an abstract which each point in the input variable is mapped to a membership value between 0 and 1.In this paper, noise is removed from an ECG signal by using subband adaptive shrinkage function using the fuzzy logic. The threshold value is selected by the fuzzy membership function for signal denoising. Among the other shrinkages functions, subband adaptive method is preferred as it produces good result by holding linearity at discontinuities. The parameters used for measuring the performance are signal to noise ratio (SNR), percentage root mean square difference (PRD), and mean square error (MSE).

Keywords

Shrinkage Function; Fuzzy Logic; Membership function; SNR; MSE

Download this article as: 

Copy the following to cite this article: Selvakumarasamy K, Poornachandra S, Amutha R. Subband Adaptive Shrinkage Function Using Fuzzy Logic. Biomed Pharmacol J 2015;8(1)

Copy the following to cite this URL: Selvakumarasamy K, Poornachandra S, Amutha R. Subband Adaptive Shrinkage Function Using Fuzzy Logic. Biomed Pharmacol J 2015;8(1). Available from: http://biomedpharmajournal.org/?p=1029

Introduction

ECG is obtained by non invasive technique which is harmless and safe in nature. The ECG signal obtained from the recording is to be properly characterized for various diagnostic purposes. Wavelet transform is found to be a useful tool for non stationary signal analysis which provide flexible environment. In the shrinkage technique, the obtained wavelet coefficients are compared with a threshold value and coefficient becomes zero when the magnitude is less than the threshold value. Threshold acts as an oracle which distinguishes significant and insignificant coefficients. Thresholding is a concept used for signal denoising.

Denoising is the process of reducing the noise from the signal and retains the signal present regardless of the frequency content of the signal. When a signal is decomposed using  a wavelet transform, two types of subbands are obtained which are lower frequency subbands and high frequency subbands. The lower frequency subbands consist of the higher details and the high frequency sub bands consist of the smaller details in the data set. If the details are small, they can be removed without affecting the main feature of the data set. By making the small details to zero, the noise present are also made zero. It becomes the basic principle of thresholding which make all frequency subbands that are less than a particular threshold to zero.

The wavelet shrinkage method was proposed by D.L.Dhono and Johnstone [1]. Soft and Hard Shrinkage method are developed for function estimation from the noisy data. In the soft shrinkage method, bias values are increased due to the shrinking of all larger coefficients towards zero by threshold value (λ). Hard shrinkage has a larger variance because of discontinuity in the function, but it has smaller bias then the soft shrinkage. Hard shrinkage are unstable in nature because it is sensitive to small changes in data [2 ]. The non negative garrote was proposed by H.Y. Gao [3]. Non garrotte shrinkage occurs when the identity line |x| becomes large; it’s continuous in nature which is used to subset regression and ridge regression.

The firm shrinkage was proposed by H.Y.Gao and A.G.Bruce. Firm shrinkage is achieved by eliminating the drawbacks of both the hard and the soft shrinkage but the disadvantages is it requires two threshold values. The hyper trim shrinkage f was proposed by S.Poornachandra and N.Kumaravel [4]. Hyper shrinkage is an optimised thresholding scheme based on universal threshold, whose major advantage is non-linearity. Hyper trim shrinkage is the one which tends to reduce the minimum mean square error between the original and denoised ECG signal. Subband   adaptive shrinkage function is proposed by S. Poornachandra and N. Kumaravel [5]. It is a nonlinear model and works on hyperbolic function which resembles the basic shrinkage distribution.

In this paper, the subband shrinkage function are proposed using the fuzzy logic. The results are compared with the hyper trim shrinkage function using the fuzzy logic [6]. The outline of this paper is as follows: Section 2 will discuss the fuzzy logic and membership function. Section 3 describes the wavelet shrinkage techniques. The experimental result are showed in section 4. Conclusion is in section 5.

Fuzzy Logic

Real world problems are too complex which increases the degree of uncertainty in the system. Traditional system analysis techniques are not exact for such problems and in order to make complexity less we introduce simple solutions is fuzzy logic which provide a satisfactory compromise between the information we have and the amount of uncertainty we are willing to accept. Fuzzy Logic was introduced by Lotfi A. Zadeh (1965), professor for computer science at the University of California in Berkeley which is used for the theory of uncertainty.

Fuzzy Logic is an abstract for a model which does not have exact boundaries and provides a mechanism for representing linguistic variable such as many, low, medium, few. Fuzzy Logic can be model as non linear functions of arbitrary complexity and it can handle problems for the unspecified or incomplete data. Fuzzy Logic provides a simple way to arrive at a definite conclusion based upon vague, imprecise, ambiguous, noisy, or missing input information. The benefits of fuzzy logic include its simplicity and its flexibility.

Fuzzy logic models, called fuzzy inference systems, consist of a number of conditional “if-then” rules.  In general, the fuzzy logic provides an inference structure that enables appropriate human reasoning capabilities.  Fuzzy logic can be applied to many applications such as Control System, Robotics, Automation, Tracking, Consumer Electronics, DBMS, Information retrieval, Pattern recognition, Machine Vision, Decision support.

Fuzzy Membership Function

A fuzzy membership function is defined as each point in the input space is represent to a membership value or degree of membership between 0 and 1 [7]. The value of membership function is discrete or continuous function and can be formed by graphical representation. The features of the membership function are core, Support and boundary which is shown in the figure 1.

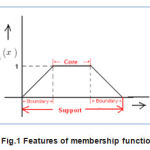Figure 1: Features of membership function Click here to View figure

 

Core: It is characterized by full membership function (1). The element which have the membership function as 1 are the elements of the core.

 

Support: It is characterized by non zero membership function. The support has the element whose membership function is greater than 0.

 

Boundary: It is characterized by non zero membership function but not full membership function. This defines the boundary of the membership function. The boundary has the element whose membership function is between 0 and 1.

 

The different types of membership function [7] are summarized in the following table 1:

Table 1: Different types of Membership Functions. Click here to View table

 

The different methods for assigning the membership values of the fuzzy logic are

Intuition

It involves the contextual and semantic knowledge about an issue. It can also involve linguistic truth value about this knowledge. It is the approximate placement of the curve on the universe of discourse, the number of curves used and the overlapping character that are the most important ideas. Inference: In this method, we use knowledge to perform detective reasoning and the membership function is formed from the facts known and knowledge.

Rank ordering

In this method, the membership values are assigned by the concept of polling method. Preference is determined by pairwise comparisons and these determine the ordering of the membership function [7].

Angular fuzzy set

It is defined on the universe of angles, repeating shapes at every 2cycles. Angular fuzzy set are applied in the quantitative description of linguistic variables.

Genetic algorithm

It uses the concept of Darwin’s theory of evolution which is based on the rule “survival of the fittest”.

Inductive seasoning

The membership values can be calculated by the characteristics of inductive reasoning which is based on the entropy minimization principles.

Neural network

It is a technique which simulates the working network of the neurons in human brain. The procedure for assigning the membership values are: first the input data set into training data set and input data set. The training data set is used to train the network and after the network is trained it is tested with the test training data. Now the neural network is used to calculate the membership values of any input data. The major drawback of neuron is the learning process.

Wavelet Shrinkage Methods

In the hard shrinkage, the wavelet coefficient are compared with the threshold value then the coefficient below the threshold value are made as zero and above the threshold value are not changes [9]. The hard shrinkage function are proposed by Donoho and Johnstone as:

 

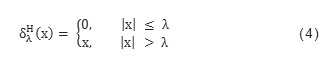
In the soft shrinkage will shrink the  coefficients above the threshold in absolute value which make smooth transitions between the original and the deleted values i.e values slightly below the threshold are not set to zero but merely attenuated. It uses the fixed thresholding as in hard thresholding method [10]. The soft shrinkage function proposed by Donoho and Johnstone are:

 

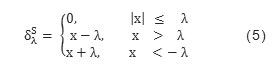
Where λ ε [0, ∞] is the threshold.

Hyper trim shrinkage is an optimized thresholding scheme based on universal threshold [4].  Poornachandra and Kumaravel (2004) proposed hyper shrinkage function as follows:

 

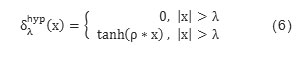
Where ρ is the boundary contraction parameter, which depends on boundary attaining parameter Δ. The parameter Δ is used to preserve the exponent behavior of shrinkage function outside redundant area of distribution curve.

The subband adaptive shrinkage functions is a nonlinear model which will work on hyperbolic function [5]. The distribution characteristics of tangent hyperbola will resembles the basic fundamental shrinkage. It exhibits antisymmetric exponential characteristics which will keep larger empirical coefficients i.e. preserve the signal characteristics and shrink the remaining empirical coefficients exponentially towards  zero. The total number of coefficients to represent the characteristics of ECG is retained so better SNR and data compression is achieved. The subband adaptive shrinkage model is expressed as

 

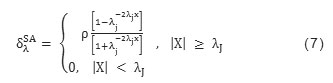
Where

 

Related Work

Fuzzy logic is a abstract which deal with reasoning that is approximate rather than fixed and exact. A fuzzy membership function defines how the input space is mapped into a membership value between 0 and 1. In this paper, the membership functions are used to choose the optimal threshold value for signal denoising. The different membership functions such as Triangle, Trapezoid, Sigmoidal, Gaussian  and Bell are used for the analysis purposes.

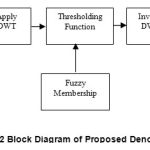Figure 2: Block Diagram of Proposed Denoised Model Click here to View figure

 

When the DWT is applied to the noisy ECG signal, we get the approximate and detailed coefficients of the signal. Then the threshold values are chosen and applied to the wavelet coefficient . Tuning of the threshold value with a fuzzy membership function is done and this threshold value will act as an oracle, which distinguishes between the significant and insignificant coefficients. The inverse DWT is applied to reconstruct the denoised signal. The block diagram of the proposed denoised model is shown in figure2.

Experimental Result

The Practical ECG signals with 1000 samples are downloaded from the PhysioBank with sampling rate 360 Hz. The simulation was carried out using MATLAB environment and tested with the various ECG signals. The performance of the subband adaptive shrinkage methods has been analyzed using the following parameter: Signal – to – Noise Ratio (SNR) and Percentage Root Mean Square Difference (PRD) [11,12].

The SNR is defined as

 

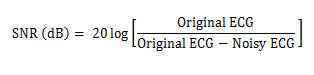
In the simulation, white Gaussian noise of different levels has been added to the original (noise free) ECG signal for testing denoising efficiency of the shrinkage functions. The different types of

Wavelet transform are used for analyzing purpose. It is found that the higher – order functions of all wavelet families produce good denoising effect. The SNR values and PRD values of the various wavelet method are calculated. Figure 2, 3 and 4 shows the SNR vs Noise value for the Hard, Soft and Subband Adaptive Shrinkage functions. The hyper shrinkage exhibits oscillatory behaviour at the ECG

signal in alternate that are suppressed in case of subband – adaptive shrinkage. Due to the increased noise level, the subband adaptive  will provide constant SNR value. The major advantage of subband – adaptive shrinkage function over hyper shrinkage is its signal stability at discontinuities, which makes the subband – adaptive shrinkage unique in its family.

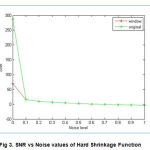Figure 3: SNR vs Noise values of Hard Shrinkage Function Click here to View figure

 

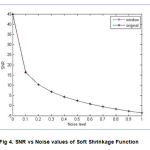Figure 4: SNR vs Noise values of Soft Shrinkage Function Click here to View figure

 

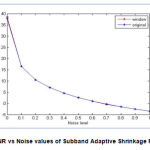Figure 5: SNR vs Noise values of Subband Adaptive Shrinkage Function  Click here to View figure

 

Conclusion

In this paper, the subband adaptive shrinkage function using fuzzy logic has been used. The subband adaptive shrinkage show how to reduce the noise distributed in the signal by shrinking the redundant empirical wavelet coefficients at every subband level. The fuzzy membership function can be used to choose the threshold value which is based on the maximum SNR, since higher value of SNR indicates the low noise. The simulation was conducted for the different level of noise using matlab. The optimal threshold and variance values have to be determined to obtain a successful signal denoising.

References

1. L. Donoho,“De-noising by Soft thresholding”, IEEE Trans. Inform. Theory 41, 1994, pp. 613–627.
2. Hong Ye Gao and Andrew G Bruce, “Waveshrink with Firm Shrinkage”, Statistica Sinica Research Report, No. 7, 1997, pp. 855 – 874.
3. -Y. Gao, Wavelet shrinkage denoising using the non- negative garrote, J. Comput. Graph. Statist. 7 (4) (1998) 469 – 488.
4. Poornachandra and N.Kumaravel, “Hyper – trim shrinkage for denoising of ECG signal”, DSP 15(2005), pp. 317-327, Elsevier.
5. Poornachandra, N. Kumaravel, “Subband – Adaptive Shrinkage for Denoising of ECG signals”, Euraship Journal on Applied Signal Processing, 2006.
6. Sri Saranya and S. Poornachandra,”Fuzzy Logic Based Thresholding for Hyper Shrinkage”, International Journal of Electrical Engineering, Volume 6, No. 4, pp. 395-403,2013.
7. N.Sivanandam, S.Sumathi and S.N. Deepa,”Introfuction to Fuuzy Logic using MATLAB”, Springer International Edition.
8. P.Soman and K.I.Ramachandran,”Insights into wavelets from theory to practice”, Prentice Hall India, New Delhi, 2002.
9. P. Zhang, M. Desai, Adaptive denoising based on SURE risk, IEEE SPIE 5 (10) (1998) 265–267.
10. G.Bruce and H.Y.Gao,”Understanding Wave shrink: Variance and bias estimation”,Biometrika 83,1996, pp. 1- 58.
11. Poornachandra, N. Kumaravel , “Wavelet based denoising using subband Dependent Threshold for ECG signals”, Digital signal processing18 (2008), pp. 49-55, Elsevier.
12. S.Poornachandra, N. Kumaravel , “Statistical estimation for Hyper   shrinkage”, Digital Signal Processing 17,   pp. 485-494, Elsevier  2006.

(Visited 810 times, 1 visits today)