N. Angayarkanni, and D. Kumar

Research Scholar Department of Electronics and Communication Engineering Periyar Maniammai University, Vallam Thanjavur - 613 403. Tamilnadu, India.

DOI : https://dx.doi.org/10.13005/bpj/628

Abstract

Breast Cancer is a serious and common disease that affects thousands of women every year in the World. Early Detection of Breast Cancer is critical for effective treatment. Mammogram is the seed stage for Mammography and Early Detection of Breast Cancer with correct screening save lives of millions of peoples in the World. Breast Cancer that Originates from inner lining of Milk ducts. Currently we have studied the location, Tissue background and Image Characteristic of Breast Cancer in three phase. First Phase we worked on converting the Gray scale image in to Binary image and in the Second Phase we described the work done for omitting the image which is having only the dark content by the usage of pixel brightness. In this paper we are described about Euclidean Distance Transformation through Image Triangulation. The results indicate that the importance of effectively displaying information in the lighter areas of the Mammogram with sufficient contrast of Mammogram Image. This approach is clearly gives the easy way to obtain the area of cancer in a breast during the screening.

Keywords

Mammogram Image; Breast cancer; Cancer detection; Medical Imaging

Download this article as: 

Copy the following to cite this article: Angayarkanni N, Kumar D. Euclidean Distance Transform (EDT) Algorithm Applied to Binary Image for Finding Breast Cancer. Biomed Pharmacol J 2015;8(1)

Copy the following to cite this URL: Angayarkanni N, Kumar D. Euclidean Distance Transform (EDT) Algorithm Applied to Binary Image for Finding Breast Cancer. Biomed Pharmacol J 2015;8(1). Available from: http://biomedpharmajournal.org/?p=1315

Introduction

Breast cancer continues to be a significant public health problem in the world and it is common cancer in women [1]. Early detection of breast cancer is the key for improving breast cancer prognosis. Currently the most effective method employed for Early Detection and Screening of Breast Cancers is Mammography [2]. However, it is difficult for radiologists to provide both accurate and uniform evaluation for the enormous Mammograms generated in widespread screening. The estimated sensitivity of radiologists in Breast Cancer screening is only about 75%, but the performance would be improved if they were prompted with the possible locations of abnormalities.

A Mammogram is basically distinct with four levels of the intensities: background, fat tissue, breast parenchyma and calcifications with increasing intensity. Masses develop from the epithelial and connective tissues of breasts and their densities on Mammograms blend with parenchyma patterns. Several studies have revealed a positive association of tissue type with Breast Cancer risks [3, 4 and 5]. Women who have breast cancers can easily get contra lateral cancers in the other side breast [6 and 7]. The traditional method for histological confirmation involves open surgery biopsy in which the breast is open and the tumor lump is fully taken out. Some women with Breast Cancer are treated with modified radical mastectomy which consist of surgical removal of a Breast Module [8]. In Both cases the surgeon does not have a real time indication or delineating the cancer cells.

There are many different proposed systems for finding of cancer cells area in Mammogram Image. The Majority of proposed cancer detection techniques in literature share the common steps to image enhancement, segmentation and quantification [9]. These techniques lie in the difficulty of analyzing the breast region, which appears different intensity level in the Mammogram Image. In the Methodology we describe about the Triangulation of making the image highly visible from the invisible background pixel and also we describe the distance calculation through Euclidean Distance transformation Algorithm.

Triangulation (Image Acquision)

In the preprocessing steps X ray film Mammogram (Gray scale) is converted in to Digital Mammogram Image .The exact pixel value depends on the range of optical densities that the scanner is capable of finding the density difference of a pixel. Delaunay triangulation is rotation and translation invariant because it consists of the direction and location only relative to its some neighboring pixel [10].Delaunay triangulation has important characteristics

1. The Delaunay Triangulation of a non degenerate set of points is unique.
2. A circle through the three points of a Delaunay triangle contains no other points.
3. If the circle is unique it is called circum circle of pixel.

Algorithm Steps

1. Take the input image as Thinned Binary image.
2. Given a set S of pixels p₁,p₂….p_N.We can compute the Delaunay Triangulation by Voronoi diagram.
3. The voronoi diagram decomposes the image in to number or regions around each pixel .Such that the entire pixel in the region around p_i closes to p_j than they are to any points in S.
4. Let P be a circle free set .three points p, q and r of P define a Delaunay triangle if there is no further point of P in the interior of the circle which is circumscribed to the triangle p, q, r and its centre lies on a voronoi vertex.
5. If any triangle has interior point the triangle replaced by new triangle.
6. Every time ensure that Triangulation is unique. This algorithm works by growing a current triangulation triangle by triangle.

In each iteration, the algorithm seeks a new triangle which attaches to the boundary of current triangulation.

Figure 1: Input Thinned Binarized Image Click here to View figure

 

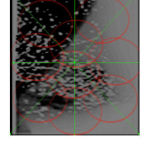Figure 2: Output Image after Triangulation Click here to View figure

 

The contrast Improvement by triangulation based on local information .So that weak regions of the image are enhanced more than strong regions. This method is beneficial to experts when manually defining the edges for diagnosing purposes. Next section we are going to discuss about the Euclidean Distance calculation between foreground and background of an image.

Euclidean Distance Transform

The Method to convert a digital binary image that consist of object (foreground ) and non object (background) pixel in to another image in which each object pixel has a value corresponding to the minimum distance from the background by a distance function is Distance Transformation. By simply exchanging the roles of Object and Background.

Distance transformation can be applied on the outside pixels of a closed boundary. Among different kinds of distance transformation the Euclidean Distance Transform [EDT] is often used because of its rotation invariance property [11]. But it involves the time consuming calculation such as square, square root and the minimum over a set of floating point numbers. To overcome these difficulties in finding of distance through Distance transformation between pixels we are going to use two scan recursive algorithms by using 3*3 neighborhoods and has analyzed. This algorithm only requires two image scans that are forward and backward rater scans in a Binary image.

Characteristic

The 8 neighbors of pixel p be denoted by  q1,q2……q8.thus N₁(p) ={q₁,q₂,q₃,q₅} and N₂(p)={q₅,q₆,q₇,q₈}.

q2	q3	q4
q1	p	q5
q8	q7	q6

 

f: A Thinned Binarized Image.

F: The set of Object pixels.

F_o : The set of Background boundary pixels.

o: The set of background boundary pixels

Q: The set of Foreground pixels which already have minimum squared Euclidean Distance through a Triangulation algorithm.

H (p, q): The Difference of the Squared Euclidean Distance of p and q (op²-oq²). qЄN₁UN_{2 .}

G (p, q): The difference of the relative coordinates of p and q.

R (p) the relative coordinate. R_x, R_y of pixel p, which records the horizontal and vertical background pixel distance between p and closet background pixel. It is initialized as all (0, 0).

 

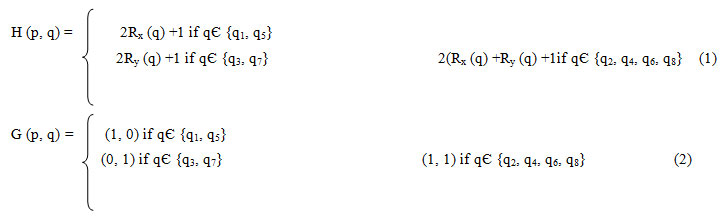
Algorithm

Forward

1. Pixel belongs to the Binary image pЄF
2. Pixel value of Binary image may be infinite. f(p)=∞
3. Select 3*3 neighboring pixel
4. If qЄN_{1 ,} q ={q₁,q₂,q₃,q₄}

4.a. f(p)=min(f(p),f(q)+H(p,q))

b. R (p) =R (q) +G (p, q)

If qЄN₂, q= {q₅, q₆, q₇, q₈}

a. f(p)=min(f(p),f(q)+H(p,q))

b. R_– (p) =R (q) +G (p, q).

E (p) = √f (p).

Case 1: The smallest squared Euclidean distance obtained from q_1.

When q₁ЄQ and o Є O

o (0,0)

q1(Rx-1,Ry)	P(Rx,Ry)	q5
q8	q7	q6

 

Using above conditions R (q₁) = ((R_x-1), R_y).Squared Euclidean Distance at q1 is oq²= (R_x-1)²+ R_y^{2 .}Squared Euclidean Distance at p will be op2= R_x²₊R_y² .Since p is located on the one pixel away from q₁.

The difference of the SED of p and q₁ according to equation (1) is

H (p, q1) = (op²-oq²)

= 2(R_x-1) + 1

This satisfies the first condition of H (p, q₁).

So R_x (q₁) = R_x-1 and G (p, q₁) = (1, 0)

R (p) = R (q₁) + G (p, q₁)

R (p) = (R (q₁) +1, R_y (q₁))

Above producer can be repeated for finding the Smallest Euclidean Distance is obtained from q₂, q₃, q_4.

Same way nearest background pixel located on the right top side also taken care for forward scan and relative coordinate R (p) was calculated.

The Smallest Euclidean Distance of p can also be obtained by another four neighborhoods q₅, q₆, q₇ and q₈ by reverse scan and R (p) was calculated.

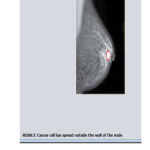Figure 3: Final Output Image with Cancer Click here to View figure

 

Conclusions

A distance transformation converts the Binary image in to Distance image. Euclidean Distance is consequently a candidate because representing images as points in a high dimensional Euclidean space, so called image space, and is a common point of most recognition algorithms. Although there is infinitely much Euclidean distance for images, they often provide counter intuitive results. Thus two scan algorithm using neighborhood Euclidean Distance Transformation algorithm use only a small image neighborhood and work with in the image itself do not need any memory. In our work we have used 3*3 neighborhoods Euclidean Distance Transformation. It is optimized and analyzed. We have implemented a set of reliable technique for Mammogram image extraction. Each pixel value is changed as a distance value shows the Mammogram Image with high level features to find the cancer cell area. Our system has potential of improving doctor’s diagnostic performance.

References

1. M. Kaczmar, N.K.P. Orzechowski, P. Iwaszko, M. Baranczyk and K.Orzechowski. Localization of Cancerous changes in Images Breast Tissue. Proceedings of the International multiconference on Computer Science and Information Technology. Vol 4, pp. 413-419, 2009.
2. H.D.Cheng, X.P. Cai, X.W. Chen, L.M. Hu and X. Lou. Computer-aided detection and classification of microcalcifications in mammograms: a survey. Pattern Recognition. Vol 36, pp.2967-2991, 2003.
3. K. Bovis, S. Singh, J. Fieldsend, C. Pinder, Identification of masses in digital mammograms with MLP and RBF nets. In: Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks Comunications. 342–347, 2000.
4. R.L. Egan and R.C. Mosteller. Breast Cancer Mammography Patterns. Cancer 40. pp. 2087-2090, 1977
5. J.N. Wolfe. Breast patterns as an index of risk for developing Breast Cancer. American Journal of Roentgenology. Vol 126, pp.1130-1139, 1976.
6. H.H. Storm and O.M. Jensen. Risk of contra lateral breast cancer in Denmark 1943-80. British Journal of Cancer. Vol.54, pp.483-492, 1986.
7. G.F. Robbins and J.W. Berg. Bilateral primary breast cancers, A Prospective Clinico Pathology. Study Cancer. Vol 17, pp 1501–1527, 1964.
8. P. Lecoq and J. Varela. Clear-PEM, A dedicated PET camera for Mammography. Journal of Nuclear Instruments and Methods in Physics Research Section A. Vol.486, pp.1–6, 2002.
9. Gonzalez, R. C. and Woods, R. E. Digital Image Processing, 3rd ed., Prentice Hall, Upper Saddle River, NJ, 2008.
10. G. Bebis, T. Deaconu and M. Georgiopoulos. Fingerprint identification using Delaunay triangulation. IEEE International Conference on Information Intelligence and Systems Proceedings. pp.452-459, 1999.
11. H.D.Cheng, X.J.Shi, R.Min, L.M.Hu, X.P.Cai and H.N.Du. Approaches for automated detection and classification of massas in mammograms. Pattern Recognition. Vol 39, pp.646-668, 2006.