M. Balamareeswaran¹ and D. Ebenezer²

¹M.E.,Communication Systems Easwari Engineering College Chennai, Tamilnadu ²Professor, Department of ECE Easwari Engineering College Chennai, Tamilnadu

DOI : https://dx.doi.org/10.13005/bpj/627

Abstract

Efficient transmission of EEG signals is necessary to optimize the performance of Brain Computer Interface (BCI) applications. This can be achieved by improving the signal to noise ratio of EEG signals. There are various methods employed in denoising such signals. Since Bio medical signals contains more redundancies it is also necessary to compress the EEG signals. For that quantization based compression schemes are used which includes complexity in the circuit. Hence Discrete Wavelet transform based Scalar Quantization (DWTSQ) is used for improving the Signal to Noise Ratio (SNR) with reduced complexity has been proposed in this project. The hybridization of quantizer with DWT transform reduces number of bits needed for storing the transmitted coefficients. The Denoised signal is classified using Immune Feature Weighted Support Vector Machine(IFWSVM) for measuring the accuracy of EEG features.. This DWTSQ increases the SNR of the transmitted signal and also produces better accuracy for different features. This is simulated using MATLAB software which gives better result than other techniques used today.

Keywords

ElectroEncephaloGraphy(EEG); Brain Computer Interface(BCI); Signal to Noie Ratio(SNR); Discrete Wavelet Transform based Scalar Quantization(DWTSQ); Immune Feature Weighted Support Vector Machine(IFWSVM)

Download this article as: 

Copy the following to cite this article: Balamareeswaran M, Ebenezer D. Denoising of EEG signals using Discrete Wavelet Transform Based Scalar Quantization. Biomed Pharmacol J 2015;8(1)

Copy the following to cite this URL: Balamareeswaran M, Ebenezer D. Denoising of EEG signals using Discrete Wavelet Transform Based Scalar Quantization. Biomed Pharmacol J 2015;8(1). Available from: http://biomedpharmajournal.org/?p=1118

Introduction

Wireless Brain Computer Interface applications plays a major role in providing better assistance to handicapped patients, mentally disabled patients, and also extends itself in tele-monitoring of patients health conditions. One such application is wireless EEG application. The electroencephalography also called as EEG is a device which records the human brain activity. Hans Berger (1929) was the first to record the human brain activity. The device is connected to the patients via various wires. The electrodes present in the EEG system records the electrical activity of human brain and transmit to the computer via wires for further processing and applications. With the development of current wireless communication system the wireless EEG recorders have been developed for measuring brain activity of moving humans [6, 13]. This wireless BCI device came  to existence in the market only recently. By optimizing it for a greater level will enhance the usage of this device to a greater extent..Wireless BCI devices does not limits its application not only for bio metric purpose[5], but also extend to Entertainment purpose and various embedded applications like driver fatigue detection and brain controlled car applications[5, 14].

Brain Computer Interface

Brain Computer Interface shortly known as BCI, is a device which functions based on the human brain waves. i.e. computing operations are performed based on the electrical recordings from the brain waves.

Optimizing  EEG Applications

The optimization of BCI applications are based on the efficient transmission of EEG signals between the subject and the embedded devices in the BCI. There are various issues like BER, degradation in SNR performance in the wireless transmission of EEG signals for BCI applications [3, 11].

Limitations in wireless BCI systems

The telecommunication parameters like Signal tom Noise Ratio plays a vital role in determining the performance of wireless BCI devices. These parameters are responsible for the enhancing the applications performance of EEG signals in wireless BCI applications. The major constraints faced by the today’s systems include:

Range of transmission

The wireless system available today suffers from transmission range

Power consumption

Normally, wireless systems have massive wires which are replaced by chargeable batteries in wireless BCI devices [9].

Output accuracy

The EEG signals comprises different features, hence transmission held in the hands of accuracy of the signals received at the receiver. The increased distance of transmission leads to more power consumption. It can be reduced by reducing the bits transmitted per sample [17].

Existing Method

The major scope of wireless BCI technique is to make the patients more convenient. The efficiency depends on reducing the noises in the signals and also compressing the signals and transmitting through the channel. These Bio medical signals consume more bandwidth because of high redundancies various techniques have been employed to overcome such problems. Most of the wireless BCI devices uses the Scalar quantization for approximating the signals. It is divided in to two major fields as Uniform quantization, non-uniform quantization and further divided as many groups [11].

Uniform Quantization

Uniform quantization is an lossy compression scheme which involves the discretization of entire signals between certain range of boundaries with equal size intervals. The range does not vary from one signal to the other and hence it has equal decision boundary.

Let us consider an source distribution with X_min, be the minimum interval value and X_max be the maximum interval  with step size taken be ∆. The M level quantizer can be designed in accordance with the eq. (1)

∆=2.Xmax/m                                              (1)

Where M represents number of levels. From [9], the MSQE for the uniform quantizer is found to be 2∆/12. The M can be taken as M=2^N levels with N no of bits.

The main disadvantage of this technioque lies in the attachment of side information which needs synchronization between transmitter and the receiver. This increases the complexity in the circuit.

Non-Uniform Quantization

The non-uniform quantizer has equal step size intervals for each signal. In this, the decision boundaries vary consequently and hence in order to design an quantizer the probability of the distributing source to be known.

In this method various parameters  like reconstruction levels has to be considered since varying decision boundaries are used which becomes the disadvantage for this method

Adaptive Uniform Quantization

In this type of backward adaptive quantization it employs an feedback from the output of the quantizer output or equally from the coded sequence of the process. In this, the quantizer boundary (step size) varies with an adjustable quantization scheme. The past output is averaged within the present input of the input sequence to the quantizer.X_min and X_max be the input quantization intervals and the variation in step size ∆ in the quantizer is given by the eq. 2,

∆=(Xmax-Xmin)/L                                  (2)

The output of the coder index I is given by the eq. 3,

I = round(( value-Xmin)/ ∆)                      (3)

Where, value is calculated from given input EEG signal.

This step size along with code word index is given as feedback path to the input quantizer. Finally, the quantized index Qo, will be the quantized value given as,

Q0 = Xmin+I*∆                                         (4)

This backward adaptive scheme requires synchronization between transmitter and the receiver which increases the complexity of the circuit.

Methodology

The EEG signals for epilepsy are collected from the Karunya University online database and it is imported in to the MATLAB software in .xls format.The collected EEG signal comprises signals for various epilepsy affected individuals for the age group comprising from 11years to 85 years. The figure (1) shows the electrode placements on the scalp of the brain and the recordings are done. The subjects are asked to sit in a quiet room and the recordings are made [14].

Normal methods uses quantization for compression of signals which is lossy compression leading to certain los of information.  In the proposed method the Discrete Wavelet Transform based quantization is used in order to filter and to compress the signal efficiently. This also reduces the complexity of the circuit.

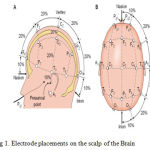Figure 1: Electrode placements on the scalp of the Brain Click here to View figure

 

Proposed method of quantization

Discrete Wavelet Transform based compression scheme employs reduction of background noise in the Bio medical signal. Because artifacts can affect the processing and transmission of EEG signals, efficient processing is necessary to increase the Signal to Noise ratio of the signal before interpretation. It is possible with the Discrete Wavelet Transform. [1, 2]. The SVM based classification efficiently classifies different features of the EEG signals which is demonstrated using the Matlab Simulation software.

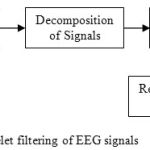Figure 2: Wavelet filtering of EEG signals Click here to View figure

 

The figure (2) shows the Discrete Wavelet Transform based filtering of Input EEG signals.. Initially the input EEG signal is decomposition block which decomposes the signal in to coefficients, then threshold it to reject the unwanted signal (high ranges) and finally reconstruct the signal. The DWT is applied to the signal with additive noise. the noisy signal is given as eq. 5,

ns = S+ AN                                     (5)

where S= EEG signal

AN= Additive noise

ns =  noisy signal

The sum of DWT of biomedical signal and noise corresponds to the DWT of noisy signal. This is the linear model of dwt based transmission.

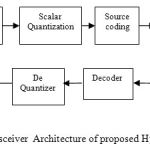Figure 3: Transceiver Architecture of proposed Hybrid Scheme Click here to View figure

 

The basic idea is that after filtering the signal, compressing is done. For that, the reconstructed signal is quantized to reduce the number of bits required to store the transformed coefficients by reducing then precision of those values. This compresses the signal to a greater extent. The proposed scheme is verified in a Transceiver architecture which includes the encoding block along with the channel and decoder part at the receiver as shown in the figure (3). The lossless coding methods like Huffman coding scheme is used. The Convolutional coder is used for transmission and decoded using Viterbi decoder which is appropriate with the encoder. Then the signal is modulated using QAM modulation and then transmitted through the AWGN channel and finally SNR is calculated for the decoded signal in order to determine the transmission efficiency of the EEG signal.

Classification of  Different Taskss

The Accuracy of the signal is measured using the classification of different features and tasks using Support Vector Machine based classifier. The original signal is denoised and compresed using DWTSQ and clasified using modified SVM.  In this modified method, Immune Feature Weighted SVM method has been used which overcomes the novel method of generalized Higuchi fractal dimension spectrum (GHFDS) which is based on multifractality of different features of EEG signals like AR features, PSD, etc [18].

SVM uses a hyper plane or set of hyper planes in a high- or infinite-dimensional space, which can be used for classification of tasks [19]. The mappings used by SVM schemes are designed to ensure that dot products may be computed easily in terms of the variables in the original space, by defining them in terms of a kernel function K(x,y)  elected to suit the problem. The hyper planes in the higher-dimensional space are defined as the set of points whose dot product with a vector in that space is constant. The vectors defining the hyper planes can be chosen to be linear combinations with parameters of feature vectors that occur in the data base. With this choice of a hyper plane, the points x in the feature space that are mapped into the hyperplane are defined by the relation:

∑αK(x,y) = constant.

Note that ifK(x,y)  becomes small as y grows further away from x.

Results

The 20 EEG signals comprising epilepsy as well as emotional signals acquired and are imported in to the Matlab software as .xls format and processed.

Input EEG signals

The EEG signals are plotted in the Matlab software as an Input signal to the designed quantization scheme and transceiver architecture. The figure (4) shows the EEG signals reflecting the working activity of six different electrodes in different colors, where data1 to data 6 refers to six electrodes signals.

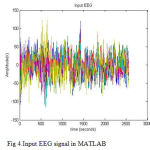Figure 4: Input EEG signal in MATLAB Click here to View figure

 

DWT components of the signal

The input EEG signals are splitted in to DWT coefficient which is shown in the figure (5).

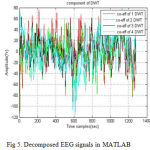Figure 5: Decomposed EEG signals in MATLAB Click here to View figure

 

DWT transform of signals

The DWT coefficients are transformed based on the DWT transform which is shown in the figure (6).

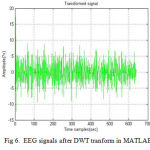Figure 6: EEG signals after DWT tranform in MATLAB Click here to View figure

 

IDWT transform

The DWT coefficients are transformed based on the DWT transform which is shown in the figure (7).

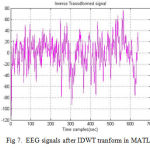Figure 7:  EEG signals after IDWT tranform in MATLAB Click here to View figure

 

Reconstruction of Signals

DWT employs multilevel decomposition and reconstruction of signals. In this method signal is divided in to three levels of complementary low pas and high pass filters. The decomposed signal is filtered using Daubechies wavelet family of order Db13 and finally the signal is reconstructed as shown in the figure (8).

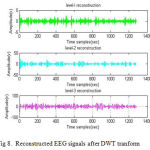Figure 8: Reconstructed EEG signals after DWT tranform Click here to View figure

Reconstructed EEG signals after DWT tranform

SNR vs BER output

The efficiency of EEG signal transmission is measured by variation of BER with varying power levels. The figure (9) and figure (10) shows the SNR Vs BER graph for the adaptive quantization and the Discrete Wavelet Transform based scalar quantization for a sample EEG signal. The test is conducted for different tasks and verified.

The SNR is calculated from the quantized signals. It is given as eq.7 and eq.8.

SNR= 10 log₁₀ (sum (value.*value)/sum (Qerr.*Qerr))         (7)

Qerr = value-Q0                             (8)

Where,

SNR- Signal to Noise Ratio

value- EEG signal amplitude before entering quantizer

Q0- quantized eeg signal

Qerr- Quantization Error

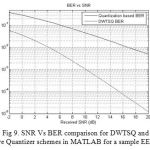Figure 9: SNR Vs BER comparison for DWTSQ and Adaptive Quantizer schemes in MATLAB for a sample EEG signal Click here to View figure

The Bit Error Rate (BER) is calculated by eq. 6,

BER= E_R/N_R                                                                                        (6)

where,

E_R– no. of error bits transmitted

N_R-total no.of bits transmitted

From the figure (10), it is shown that the BER for the wavelet quantizer scheme is about 10^-5for the given SNR at 20 dB. Whereas the adaptive quantization scheme is about only 10^-2.. hence the transmission scheme has better transmission efficiency than the existing Uniform quan tization scheme.

Classification using  Immune Feature weighted SVM

The Diseases and different tasksfrom EEG signals is challenging because EEG signals are non-stationary and nonlinear.Support vector machine (SVM) method has been widely used as a classification tool. The SVM parameters and the kernel function also affect classification accuracy. Immune feature weighted SVM (IFWSVM) method was proposed to improve the accuracy of classification. Immune algorithm (IA) uses kernel functions (weighted vectors) which finds the optimal feature weighted with additional featureslike Entropy and standard Deviation..

The Table 1 gives the classification of some of thesample EEG signals which is reconstructed using Discrete wavelet Transformand quantized using Scalar Quantization and their accuracy baed on Immune Weighted SVM method.

Table 1:Accuracy of Different tasks classified

S.No	Tasks	Accuracy	STD
1.	Happy	100%	0
2.	Sad	91.89%	11.59
3.	Fear	100%	0
4.	Epilepsy	98.42%	3.16
5.	Aneurysm	97.89%	4.21
6.	Brain disorder	97.78%	4.44

 

The figure (10) shows the classified signal using IFWSVM which shows the accuracy of 100%.

Figure 9B: Aneurysm(disease) Task which is classified using SVM Click here to View figure

 

Conclusions

The modified Discrete Wavelet Transform based Quantizer, the transmitted EEG signals show the better SNR of EEG signals than the existing adaptive quantizing scheme. The discrete wavelet transform is used for de noising efficiently the EEG signals efficiently. Normally wavelet transform or quantizer is used for compression of signals. But in this proposed hybrid technique quantization of reconstructed signal using wavelet transform reduces the number of bits needed for transmission by precision more effectively. The wavelet transform is successfully simulated in a Transceiver design using MATLAB software.  By means of development of efficient transmission of EEG signals, the patients can be benefitted with the wireless BCI applications in telemedicine field. Not only in telemedicine field, but also in gaming and in Brain controlled embedded application, it plays a vital role.

In the Future, the proposed Hybrid system can be used for the real time implementation of Driver fatigue warning application of brain waves. Based on the efficient processing of the eye movement of the drivers, it is possible for giving the best fatigue warning systems based on brain waves.

Acknowledgment

We would like to extend our sincere thanks to Easwari Engineering College and to all members of Research Group at ECE Department, Anna University, for their constant supports and encouragement.

References

1. Jonathan, Bradley, N., Christopher, Brislawn, M. FBI wavelet Scalar quantization for Fingerprint Image compression. SPIE proceedings.,1993;203-04.
2. Dora, Ballesteros, M.,  Andrés,. Gaona and Luis, Pedraza F. Discrete Wavelet Transform in  Compression and Filtering of  Biomedical Signals. INTECH Europe .
3. Mahsen Habib Nezhad, Khazaimatol, S., Mehran Yahyavi. Improvement of wireless transmission system performance for EEG signals based on development of scalar quantization. Journal of electrical Bio-impedence, Vol.52, 2013;  2032-46.
4. Scher, M.S. Automated EEG-sleep analyses and neonatal neurointensive care Sleep Medicine. 2004; 5(6): 533-40. http://dx.doi.org/10.1016/j.sleep.2004.07.002
5. Michel, C.M.,  Murray, M.M., Lantz, G., Gonzalez, S., Spinelli, L. Grave de Peralta, R. EEG source imaging. Neurophysiol, 2004;2195-2222.
6. Tolbert, J.R., Kabali, P., Brar, S., Mukhopadhyay, S. A low power system with adaptive data compression for wireless monitoring of physiological signals and its application to wireless electroencephalograph. International Symposium on Quality Electronic Design (ISQED), San Jose, CA. USA, 2010;.333-41.
7. Argyropoulos, S., Tzovaras, T., Ioannidis, D., Damousis, Y., Braun, M., Boverie, S. Biometric template security in multimodal biometric systems based on error correcting codes.Journal of Computer Security, 2010; 161–85.
8. S. Sanei, J.A. Chambers, EEG Signal Processing,, Wiley Interscience: New York, 2007.http://dx.doi.org/10.1002/9780470511923
9. Abaya, E.F., Wise , G.L. On the Existence of optimal quantizers. IEEE Trans. Information Theory, 1982;937-40.
10. Sayood, K., Na, S. Recursively indexed quantization of memoryless sources. IEEE Transactions on Information Theory, 1996; 1602-09.
11. Lin, C.T., Chen, Y.C., Huang, Y., Chiu, T.T., Ko, L.W., Liang, S.F. Development of wireless brain computer interface with embedded multitask scheduling and its application on real-time driver’s drowsiness detection and warning. IEEE Trans.Biomed. Eng, 2008; 1582-91.
12. K. Sayood Introduction to data compression. 3. ed. Elsevier:NewYork. 2006.
13. Callan, D., Gamez, M., Cassel, D., Kawato, M. Dynamic visuomotor transformation involved with remote flying of a plane utilizes the ‘Mirror Neuron’ system. PLoS One, 2012; 1-14.
14. Chi, M., Wang, Y., Maier, C., Jung, T.P., Cauwenberghs, G. Dry and noncontact EEG sensors for mobile brain–computer interface.IEEE Trans. Neural Systems and Rehab. Eng,2012; 228–35.
15. Palaniappan, R., Mandic, D.P. Biometrics from brain electrical activity. A machine learning approach. IEEE Trans. Pattern Analysis and Machine Intelligence, 2007;738-42.
16. Abdullah, M.K., Subari, K.S., Loong, K.L., Ahmad, N.N. Analysisof the EEG signal for a practical biometric system.World Academy of Science, Engineering and Technology, 2010; 1133-37.
17. Wang, A., Sodini, C. A simple energy model for wireless microsensor transceivers. IEEE Global Telecomm Conf., Texas,USA, 2005; 3205-09.
18. Qiang Wang and Olga Sourina. Real time mental Arithmetic Task Recognition from EEG signals. IEEE Transactions on Neural systems and Rehabiliation Engineering,Vol.21, No.2, 2013; 225-32.
19. Matthias Kaper Peter Meinicke, Ulf Grossekathoefer, Thomas Lingner, and Helge Ritter. BCI Competition 2003—Data Set IIb: Support Vector Machines for the P300 Speller Paradigm. IEEE Transactions On Biomedical Engineering, 2004;  1073-76.