Hadi Rezaee¹, Zahra Shakarami¹,Mohammad Hosseini²,Mansour Zabihzadeh^1,2*, Mostafa Feghhi³

¹Department of Medical Physics, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. ²Department of Radiation Oncology, Golestan Hospital, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. ³Department of Ophthalmology, Imam khomeini Hospital, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, Iran. *Corresponding author: Email: zabihzadeh@ajums.ac.ir

Abstract

Accurately determination of dosimetric parameters for low-energy ¹⁰³ Pd source is crucial to use by treatment planning systems. The dosimetric parameters such as the air kerma strength, S_k, dose rate constant, L, radial dose function, g(r) and anisotropy function, F(r, q) for  the low-energy ¹⁰³ Pd source were investigated. MCNPX (2.6.0) simulation code was used to calculate all dosimetry parameters. Full details of Theragenices-¹⁰³ Pd source model 200 (dimentiones, materials and energy spectrum) were implementd in MC simulations. The ¹⁰³ Pd source was centered in infinite water phantom and the radial dose function calculation the dose was scored in concentric rings with different thickness bonded by 88^° and 92^° conics. Due to symmetry of source geometry and in order to reducing of errors, the 0.5 mm thickness rings were bounded with two oblique cones (with interval angel of 1°) from 0° to 90° in order to calculate Anisotropy function. The air kerma strength, S_k and dose rate constant, L were found equal to 0.646 cGycm²h^-1mCi^-1 and 0.798 cGyh^-1U^-1, respectively. For radial dose function, g(r), using an equation as g(r) = a₀+a₁r+a₂r²+a₃r²lnr+ a₄/r², Where a₀=1.6440, a₁=-0.8338, a₂=0.1917, a₃=-0.0539, a₄=-0.0062 with R²=0.9995 have been yielded a better fitting than the fifth-order polynomial equation recommended by AAPM, TG-43U1. The calculated anisotropy values included the distances of clinical interest for this type of low-energy photon source, up to 2 cm, and especially for smaller angles, q<20°, were estimated by different fifth-order polynomial equations with R²>0.9935. The calculated results and extracted equations are in good agreement with the corresponding values reported by AAPM, TG-43U1 and can be used in Monte Carlo based treatment planning system.

Keywords

Brachytherapy; ¹⁰³ Pd (Theragenics, Model 200) Source; Monte Carlo Simulation; Dosimetry  

Download this article as: 

Copy the following to cite this article: Rezaee H, Shakarami Z, Hosseini M, Zabihzadeh M, Feghhi M. Dosimetric Characteristics of 103 Pd (Theragenices, Model 200) Brachytherapy Source. Biomed Pharmacol J 2015;8(March Spl Edition)

Copy the following to cite this URL: Rezaee H, Shakarami Z, Hosseini M, Zabihzadeh M, Feghhi M. Dosimetric Characteristics of 103 Pd (Theragenices, Model 200) Brachytherapy Source. Biomed Pharmacol J 2015;8(March Spl Edition). Available from: http://biomedpharmajournal.org/?p=2239>

Background

The ¹⁰³ Pd (Theragenics, Model 200) brachytherapy source introduced by Theragenic Company in 1987 and is used as first interstitial ¹⁰³ Pd source (1). The ¹⁰³ Pd source is widely used in prostate permanent implants and for the treatment of malignant tumors in the eye due to the rapid decrease in dose with radial distance because of its low energy emissions (20 keV) and the higher dose rates due to the short half-life (17 days) than other alternative source such as ¹²³I (2, 3).

Such brachytherapy treatments include lower side effects compared to photon or electron teletherapy. The high dose gradient at the small radial distances and the influence of source anisotropy on dose distribution around the source (especially along the longitudinal axis) dictate high degree accuracy for dosimetry of ¹⁰³ Pd. There are some complications during practical dosimetry of brachytherapy sources such as not completely tissue equivalent of solid phantoms and dosimeters, lack of needed resolution due to large size of dosimeters, energy dependence of dosimeters and etc. Accurately determination of dosimetric parameters for ¹⁰³ Pd source is crucial to use by treatment planning systems (TPS) for clinical implementation (4, 5).

In this work, the recommended dosimetric parameters by AAPM, TG-43 (6) such as the air kerma strength, S_k, dose rate constant, L, radial dose function, g(r) and anisotropy function around the ¹⁰³ Pd source model 200 have been estimated by means of MCNPX code.

Objectives

The dosimetric parameters such as the air kerma strength, S_k, dose rate constant, L, radial dose function, g(r) and anisotropy function, F(r, q) for the low-energy ¹⁰³ Pd source were investigated.

Materials and Methods

Dose Calculation Formalism as Recommended by AAPM TG-43U1

As recommended by the AAPM Radiation Therapy Task Group no. 43 (6), the dose rate at a given point (r, q) around the cylindrical symmetry source relative to the geometric center of the source is given by

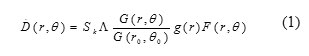
Where r is the radial distance from the source center to the point of interest, q is polar angle with respect to the longitudinal axis of the source, S_k is the air-kerma strength in unit of U=cGy cm² h^–1, L is the dose rate constant in unit of cGy h^–1 U^–1, G(r, q) is the geometry factor that accounts for the spatial distribution of the radioactive material, g(r) is the radial dose function that accounts for radial appendence of photon absorption and scatter in the medium along the source longitudinal axis, F(r, q) is the anisotropy factor that accounts for the radial and angular dependence of photon absorption and scatter in the medium and the reference point (r₀, q₀) is located on the transversal axis at r₀=1 cm and q₀=p/2 (6, 7). The dosimetric parameters inserted in Eq. 1 that were investigated in this study followed by

 

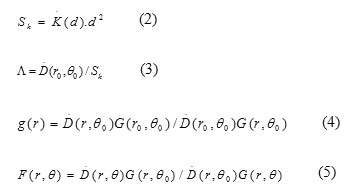
A detail description of the formalism can be found in AAPM, TG-43 report.

MC Calculations Techniques 

Dose distributions in this work were simulated with the MCNPX (2.6.0) Monte Carlo (MC) radiation transport code published by Los Alamos National Laboratory (8). The MCPLIB04 photon cross-section library based on the ENDF/B-VI data and the EL03 electron cross-section library were used.

The MCNPX cell energy energy fluence estimator (*F4 tally, MeV/cm²) was used to determine air kerma rate, . In the Monte Carlo cal­culations, it was assumed that all electrons generated by the photon collisions are absorbed locally due to the low energy of the photons from ¹⁰³Pd, so it was considered that dose is equal to kerma at all points of the water phantom. The MCNPX track –length estimator (F6 tally, MeV/gr) was used to determine the dose rate distribution in water and subsequently the dosimetric parameters such as g(r), F(r, q) and  (1, 9). The Rayleigh scattering, Compton scattering, fluorescent emission of characteristic K-shell and L-shell X-rays and photoelectric absorption are all modeled in calculations. The energy cut off of the photon transport was set to 5 keV to reduction in computing time since the number of events to be simulated is reduced (7, 9). In order to the better level of confidence no variance reduction technique was used in simulations. No source beta electrons were implemented in calculations due to their negligible chance to penetrating from the titanium capsule .

¹⁰³ Pd Source Characteristics 

The ¹⁰³ Pd source (Theragenics, Model 200) include of two cylindrical graphite (2.22 g/cm³) with diameter of 0.56 mm and length of 0.890 mm coated with thin layer of radioactive palladium (12.033 g/cm³) with thickness of 2.2 μm (figure 1). Figure 1 shows a schematic diagram of the ¹⁰³ Pd source.  A lead marker (11.4 g/cm³) with length of 1.09 mm and diameter of 0.5 mm was located between this two graphite parts. These parts were capsulated inside a cylindrical titanium capsule (4.51 g/cm³) with external diameter of 0.826 mm and thickness of 0.056 mm. The each ends of source were closed with 0.334 mm length of a cylindrical shield and with a titanium cup part. These two end weld parts have internal diameter of 0.306 mm and thickness of 0.04 mm. The total and active lengths of this source were 4.5 mm and 4.23 mm, respectively (10).

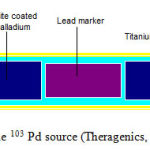Figure 1: The 103 Pd source (Theragenics, Model 200) Click here to view full figure

The ¹⁰³ Pd photon spectrum used in the simulation, table 1, was taken from AAPM TG-43U1 (6).

Table 1: The photon spectrum of ¹⁰³Pd source, used in the simulation.

Photon energy (keV)	Photon per integrations (%)
20.074	0.224
20.216	0.423
22.72	0.104
23.18	0.0194
39.75	0.00068
294.98	0.00003
357.5	0.00022
497.1	0.00004

Air Kerma Strength, S_k

For the source air-kerma strength estimation, the ¹⁰³ Pd source was centered in a vacuum sphere with radius of 150 cm and surrounded by an air ring detectors of 1 cm height and 1 cm thickness. In order to minimize the fluctuation, the inner radius of the air ring detector was changed from 10 to 100 cm with interval of 10 cm in separate programs and average of them was reported as the air kerma rate (6, 7).

Radial Dose Function, g(r)

For dose estimation, a large enough cubic water phantom with dimensions of 30 cm³ was considered in order to reach full scatter conditions (4). For the radial dose function, g(r), calculation, the ¹⁰³ Pd source was centered in water phantom and the dose was scored in concentric rings with thickness of 0.5 mm for radial distances less than 0.3 cm, 1mm for radial distances from 0.3 to 1cm, 5 mm for radial distances from 1 to 10 cm (4, 11-13). The rings were bonded by 88^° and 92^° conics along the transversal axis of the source to compromise between the desired accuracy and the spatial resolution of the calculated dose.

Anisotropy Function, F(r, q)

The water phantom was divided by concentric rings with thickness of 0.5 mm on the included plan of longitudinal axis of centered source in the phantom. Due to symmetry of source geometry and in order to reducing of errors, the rings were bounded with two oblique cones (with interval angel of 1° to minimize of averaging volume) from 0° to 90°, however only ones around the 0°, 10°, 20°… 90° have been reported in results (5). To minimize statistical uncertainties to become insignificant, 1´10⁸ photon histories were simulated for the air-Kerma strength and 1´10⁹ photon histories for the radial dose function and anisotropy function. The statistical uncertainties on the absorbed dose in varied from 0.1% to 2% for distances lower than 5 cm and rising to 5% at 9 cm.

Results and Discussion

The air kerma strength of the ¹⁰³ Pd source (Theragenics, Model 200), S_k, was calculated including the titanium X-ray emission and was S_k= 0.646 cGycm²h^-1mCi^-1 by the extrapolation method. Our calculated air kerma strength is in good agreement with one reported by Monroe & williamson (2002) (1), 0.633 cGycm²h^-1mCi^-1 for this model of ¹⁰³ Pd source, however, discrepancy of %2 cGycm²h^-1mCi^-1 can be mainly caused by the little difference of the applied photon spectra and cross section libraries in two sets of simulations. In another published data by Williamson (2000) (14), for the same source but with radioactive palladium layer of 2 μm thickness, the air kerma strength was reported as 0.639 cGycm²h^-1mCi^-1. In average, the S_k reported for this source by the WAFAC method is approximately %12 greater than with ones estimated by extrapolation manner.

The calculated dose rate constant, L was compared with others published data in Table 2. Our result with extrapolation, 0.798 cGyh^-1U^-1, was in the best agreement (discrepancy of 0.12 %) with one reported by Monroe & williamson (2002) (1), 0.797 cGyh^-1U^-1. Due to thinner radionuclide coating on the Graphite for the source investigated by Williamson (2000) (14), the dose rate constant was less than, 2.8%, in comparison to the used source herein. Difference of 12 to 15% was resulted between extrapolation method compared to the ones calculated by the WAFAC method that indicate a high dependence of air kerma strength and dose rate constant calculation to the used method.

Table 2: Comparison of dose rate constant values, L, for the ¹⁰³ Pd source (Theragenics, Model 200).

Ratio	Ʌ(cGyh-1U-1)	Method	TeraGenic 103Pd source	References
0.97	0.776	Extrapolation	200(2mµ)	Williamson (2000) (14)
1.00	0.797	Extrapolation	200(2/2mµ)	Monroe & williamson (2002)(1)
0.86	0.686	WAFAC	200(2/2mµ)	AAPM, TG-43 (2004)(6)
0.86	0.688	WAFAC	200(2mµ)	Williamson (2000)(14)
0.87	0.691	WAFAC	200(2/2mµ)	Monroe & williamson (2002)(1)
—	0.798	Extrapolation	200(2/2mµ)	This work

The calculations of the radial dose function, g(r), for 0.1< r < 9 cm in water phantom are presented in Table 3 along with the corresponding quantitative data reported by Taylor et al. (2007) (15), TG-43U1 (2004) (6) and Williamson (2000) (14). Our data for g(r) relatively are in good agreement with previously published data. For distances smaller than 1 cm our results agrees within 1.5% with the ones reported by other researchers, however the best agreement across r<1 cm for 200 (2.2 μm) model was obtain with the ones reported by AAPM, TG-43U1 (2004) in averaged discrepancy of 1.3%. For greater radial distances from 1 cm to 5 cm our values are much closer to that from AAPM, TG-43U1 (2004) than Taylor et al. (2007) with averaged discrepancies of 5.0 and 6.4%, respectively. For greater distances from 5 to 9 cm these discrepancies slightly increased and reached to 5.3 and 7.2%, respectively. Using of different cross-sections libraries by different MC codes could be as the main source for these discrepancies, as may be seen our results from MCNPX code basis on ENDF/B-VI cross-section library are in better agreement with AAPM, TG-43 reported data than ones calculated by Taylor et al. (2007) (15) with EGSnrc code. The differences in some elements such as tally volumes cut off kinetic energy of photon and electron, dimensions, compositions and density of simulated materials and the primary photon spectrum of the source could have a small role of these discrepancies.

Table 3: MC calculated radial dose function values, g(r), for the Theragenics-¹⁰³Pd source model 200.

Radial distance (cm)	Taylor et al. (2007)	AAPM, TG-43U1 (2004)	Williamson (2000)	This work
0.1	0.928	0.911	0.904	0.945
0.2	1.339	—	—	1.311
0.3	1.338	1.38	1.319	1.380
0.4	1.363	1.36	1.296	1.292
0.5	1.308	1.30	1.255	1.253
0.6	1.244	—	1.212	1.211
0.7	1.179	—	—	1.165
0.8	1.112	—	1.106	1.106
0.9	1.058	—	—	1.052
1	1.00	1.00	1.00	1.000
1.5	0.741	0.749	0.753	0.778
2	0.551	0.555	0.557	0.582
2.5	0.406	0.410	0.410	0.432
3	0.298	0.302	0.301	0.319
3.5	0.219	0.223	—	0.235
4	0.160	0.163	0.163	0.172
4.5	0.117	—	—	0.127
5	0.0865	0.0887	0.0882	0.093
6	0.0469	0.0482	0.0484	0.051
7	0.0256	0.0262	—	0.028
8	0.0147	—	—	0.016
9	0.00837	—	—	0.009

As recommended by AAPM, TG-43 report, a fifth-order polynomial fit into the calculated MCNPX radial dose function in water for a radial distance from 0.1 to 9 cm (see figure 2) yielded the following equation: gL(r) = a₀ + a₁r + a₂r² + a₃r³ + a₄r⁴+ a₅r⁵, where a₀ = 1.25, a₁ = – 0.0088, a₂ = – 0.2829, a₃ = 0.0862, a₄ = – 0.009, and a₅= 0.0004, define R² = 0.9737. As can be seen from figure 2, a fifth-order polynomial fit in radial distances smaller than 1 cm not yielded a good prediction for our calculated radial dose function values or other reported data by Taylor et al (2007) (15), TG-43U1 (2004) (6). However this fit basis our or AAPM, TG-43U1 data resulted relatively good estimation for g(r) at radial distances greater than 1 cm but overestimation of ~32% for g(r) at radial distance of 0.1 cm and ~6% averaged underestimation for distance from 0.2 to 0.8 cm should not be completely adequate for clinical calculations; especially for intravascular brachytherapy that needs high accuracy of dose distribution at the closed distances to the source. Therefor to reach better estimation of radial dose function values for this  source, a following simple equation is recommended as g(r)=a₀+a₁r+a₂r²+a₃r²lnr+ a₄/r², Where constant coefficients basis on our data and with good approximation with those reported by AAPM, TG-43U1 were a₀=1.6440, a₁=-0.8338, a₂=0.1917, a₃=-0.0539, a₄=-0.0062, define R²=0.9995

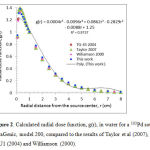Figure 2. Calculated radial dose function, g(r), in water for a 103Pd source TeraGenic, model 200, compared to the results of Taylor et al (2007), TG-43U1 (2004) and Williamson (2000). Click here to view full figure

 

The calculated anisotropy dose function values, F(r, q) are shown in Table 5 for radial distances from 0.5 to 5 cm and for angles between 0° to 90° in intervals of 10°.  Figure 3 shows the anisotropy dose function values of ¹⁰³Pd source model 200 in comparison with the experimental data measured by AAPM, TG-43U1 and Yu & Nath (2002) and the calculated values using EGSnrc code by Weaver (1998) (5) and Taylor et al. (2007) (15). Our results for anisotropy function are in relatively good agreement with ones reported by AAPM, TG-43 (2004) and Taylor et al. (2007). For distances of clinical interest for this type of low-energy photon source, up to 2 cm, the average difference between our data and those of AAPM, TG-43 (2004) and Taylor et al. (2007) was smaller than 6, 2 and 3% for radial distances of 0.5, 1 and 2 cm, respectively. In this range of radial distance, our data are considerably lower and higher than that of results measured by Yu & Nath (2002) and calculated by Weaver (1998), respectively. The reactor-produced ¹⁰³Pd that was investigated in AAPM, TG-43U1 (2004) and in the present study has relatively lower specific activity than the cyclotron-produced ¹⁰³Pd that was studied by Yu and Nath (2002) and Weaver (1998). The difference of fabrication can lead to such large discrepancies between these two Theragenics model 200 ¹⁰³Pd sources.

Due to low average energy of ¹⁰³Pd source, 20.74 KeV, the source results a strong anisotropy along its long longitudinal axis (first row for q=0° from table 4). The high gradient for dose anisotropy especially for shorter distances and small angles is mainly due to the source self-absorption and oblique filtration of photon through the capsule, marker and end caps that is enhanced by low energy spectrum of ¹⁰³Pd source.  Therefore, the anisotropy dose calculations and measurements for this type of source are extremely depends to the tally size or to the dosimeter size for the reasons as discussed above. A compromise between tally volume and number of histories, particularly along the longitudinal axis, is needed to reach acceptable uncertainties for data from the simulations. For the presented calculations, no variance reduction technique was used; instead our scouring ring volumes with same thickness of 0.5 mm were increased by increasing radial distance due to diverging of two oblique cones around the desired angle with interval of 1°.  As a result of this technique the uncertainties obtained are smaller than 5%. In spite of what for the radial dose function, a fifth-order polynomial fit on anisotropy values has been resulted relatively good prediction for F(r, q), with R²> 0.9935.

Table 4: Anisotropy dose function, F(r, q) calculated for ¹⁰³ Pd source.

Angle, q (deg)	Radial distance from center of source (cm)
	0.5	1	2	3	4	5
0	0.632	0.512	0.497	0.482	0.474	0.502
10	0.443	0.464	0.483	0.498	0.499	0.536
20	0.492	0.488	0.519	0.548	0.553	0.573
30	0.643	0.589	0.605	0.624	0.637	0.622
40	0.764	0.728	0.735	0.750	0.751	0.732
50	0.815	0.831	0.831	0.842	0.848	0.831
60	0.947	0.908	0.903	0.912	0.921	0.910
70	0.991	0.956	0.957	0.956	0.999	0.998
80	1.002	0.990	0.998	1.010	1.020	1.020
90	1.000	1.000	1.000	1.000	1.000	1.000

 

 

Figure 3: Comparison of the calculated anisotropy dose function, F(r, q) of the Theragenics- 103Pd seed model 200 with other published data. Click here to view full figure

 

Conclusion

The dosimetric parameters recommended by AAPM, TG-43U1 that are need for clinical brachytherapy treatment planning such as the air kerma strength, S_k, dose rate constant, L, radial dose function, g(r) and anisotropy function, F(r, q) were calculated for the low-energy ¹⁰³ Pd seed (Theragenices, model 200) using the MCNPX (2.6.0) simulation code. The values of air kerma strength and dose rate constant for the Theragenics, model 200 ¹⁰³Pd source estimated to be 0.646 cGycm²h^-1mCi^-1 and 0.797 cGyU^-1h^-1, respectively which were in good agreement with the ones reported by Monroe & williamson (2002) as 0.633 cGycm²h^-1mCi^-1 and 0.798 cGyU^-1h^-1. Our data for g(r) are in good agreement with previously data published by AAPM, TG-43U1 (2004) in averaged discrepancy of 1.3% for r<1cm, 5.0% for 1cm<r<5cm and 5.3% for 5cm<r<9 cm. instead of a fifth-order polynomial equation a simple equation g(r) =a₀+a₁r+a₂r²+a₃r²lnr+ a₄/r² is recommended to fitting of radial dose function values. Our results for anisotropy function are in relatively good agreement with ones reported by AAPM, TG-43 (2004) and Taylor et al. (2007). The high gradient for dose anisotropy especially for shorter distances and small angles is mainly due to the source self-absorption and oblique filtration of photon that is enhanced by low energy spectrum of ¹⁰³Pd source.  Therefore, the anisotropy dose calculations for this type of source are extremely depends to the tally size.

Acknowledgment

This study is part of M.Sc thesis for Hadi Rezaee Special thanks to Ahvaz Jundishahpur University of Medical Sciences for the financial support (grant no. IORC-9201).

Financial Disclosure

There is no financial disclosure.

Reference

1. Monroe JI, Williamson JF. Monte Carlo-aided dosimetry of the theragenics TheraSeed model 200 103Pd interstitial brachytherapy seed. Medical physics. 2002;29(4):609-21.
2. Reniers B, Verhaegen F, Vynckier S. The radial dose function of low-energy brachytherapy seeds in different solid phantoms: comparison between calculations with the EGSnrc and MCNP4C Monte Carlo codes and measurements. Physics in medicine and biology. 2004;49(8):1569.
3. Potters L, Morgenstern C, Calugaru E, Fearn P, Jassal A, Presser J, et al. 12-year outcomes following permanent prostate brachytherapy in patients with clinically localized prostate cancer. The Journal of urology. 2005;173(5):1562-6.
4. Rodríguez EA, Alcón EP, Rodriguez ML, Gutt F, de Almeida E. Dosimetric parameters estimation using PENELOPE Monte-Carlo simulation code: Model 6711 a ¹²⁵ I brachytherapy seed. Applied radiation and isotopes. 2005;63(1):41-8.
5. Weaver K. Anisotropy functions for 125I and 103Pd sources. Medical physics. 1998;25(12):2271-8.
6. Rivard MJ, Coursey BM, DeWerd LA, Hanson WF, Huq MS, Ibbott GS, et al. Update of AAPM Task Group No. 43 Report: A revised AAPM protocol for brachytherapy dose calculations. Medical physics. 2004;31(3):633-74.
7. Awan SB, Dini SA, Hussain M, Meigooni DS, Meigooni AS. Cylindrical coordinate based TG-43U1 parameters for dose calculation around elongated brachytherapy sources. Journal of Applied Clinical Medical Physics. 2008;9(2).
8. Briesmeister JF. MCNPTM-A general Monte Carlo N-particle transport code. Version 4C, LA-13709-M, Los Alamos National Laboratory. 2000.
9. Saidi P, Sadeghi M, Shirazi A, Tenreiro C. Dosimetric parameters of the new design ¹⁰³Pd brachytherapy source based on Monte Carlo study. Physica Medica. 2012;28(1):13-8.
10. Taylor R, Rogers D. An EGSnrc Monte Carlo-calculated database of TG-43 parameters. Medical physics. 2008;35(9):4228-41.
11. Li Z. Monte Carlo calculations of dosimetry parameters of the Urocor Prostaseed I-125 source. Med Phys 2002;29(6):1029-34.
12. Rivard MJ. Comprehensive Monte Carlo calculations of AAPM Task Group Report No. 43 dosimetry parameters for the Model 3500 I-Plant I-125 brachytherapy source. Applied Radiation and Isotopes 2002;57:381–9.
13. Sowards KT, Meigooni AS. A Monte Carlo evaluation of the dosimetric characteristics of the Bests Model 2301 I-125 brachytherapy source Applied Radiation and Isotopes   2002;57:327–33.

14. Williamson JF. Monte Carlo modeling of the transverse-axis dose distribution of the Model 200 103Pd interstitial brachytherapy source. Medical physics. 2000;27(4):643-54.
15. Taylor R, Yegin G, Rogers D. Benchmarking brachydose: Voxel based EGSnrc Monte Carlo calculations of TG-43 dosimetry parameters. Medical physics. 2007;34(2):445-57.

 

(Visited 462 times, 1 visits today)