Medetbekova R. A, Nyssanov Y. A, Zhumakhan M, Medetbekov M. M, Lyazzat Z. Solution for Permanent Flow of An Ideal Biphasic Medium in Open Channels of a Constant Cross Section. Biomed Pharmacol J 2014;7(1)

---

Manuscript received on :
Manuscript accepted on :
Published online on: 22-12-2015

---

Plagiarism Check: Yes

How to Citeclose    |   Publication History close

 Views: (Visited 72 times, 1 visits today)    PDF Downloads: 496

Ryskul Ashimaliyevna Medetbekova¹, Yernazar Aidarovich Nyssanov², Myrkhalykov Zhumakhan³, Muratbek Mukhalbekovich Medetbekov¹ and Zhaydakbayeva Lyazzat⁴

¹The Candidate of Science (Physics and Mathematics), Head of the Chair, M.Auezov South Kazakhstan State University, Shymkent, Kazakhstan.

²The Doctor of Science (Physics and Mathematics), M.Auezov South Kazakhstan State University, Shymkent, Kazakhstan.

³Doctor of Engineering Science,professor, rector of M.Auezov South Kazakhstan State University,160012, Shymkent , Taukekhan avenue, 5, Republic of Kazakhstan.

⁴The Candidate of pedagogical science, M.Auezov South Kazakhstan State University, faculty of information technology, Shymkent, Taukekhan avenue, 5, Kazakhstan.

DOI : https://dx.doi.org/10.13005/bpj/469

Abstract

Water used for irrigation contains solid particles, which significantly affect macroscopic parameters, mechanical properties, flow, and water-treatment processes. This paper presents a solution to the challenge of achieving a permanent flow of an ideal biphasic medium in the open channels of a constant cross section by using an interpenetrating model of a biphasic medium. We present analytical expressions for phase speed and concentration of a two-component medium for the first time and derive relationships between speed and density of components.

Keywords

Biphasic medium; Open channels; constant cross section

Introduction

Over the past few years, hydrodynamics has seen many advances in the area of investigation into the dynamics of flow in open channels (Nyssanov 2005). However, the models used in studies for this area do not completely cover the physics of the process because in Central Asia, the water used for irrigation is not homogenous and contains a number of hard particles. The presence of small amounts of hard particles in water flow, as is known, considerably modifies the character and structure of the water-treatment processes (Abalyants 1981). Recently discovered microscopic parameters, in particular density, interact with the power between phases as well as other mechanical characteristics. These flow parameters work against the maintenance of mixture components and the components interrelate, which cause a redistribution of the speed and concentration of the separate components, and changes the expenditure of a mixture.

In light of these problems, the modern mechanics of a continuous medium is an important issue for investigation in terms of the movement of a multiphase medium.

This task is addressed in this paper by using an interpenetrating model of a biphasic medium, in accordance with which the equation of movement has its own appearance (Nigmatullin 1987; Umarov and Akhmedov 1989)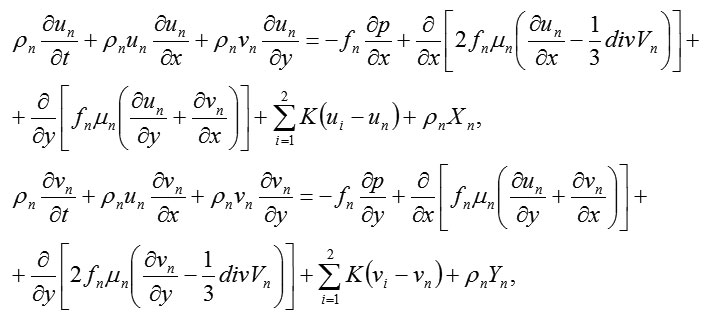

as well as the equation of continuity

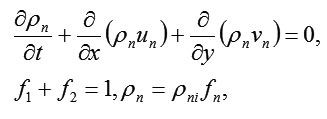
where, ρ_n , ρ_ni  the provided and real density of the n-phase, respectively;

u_n- the longitudinal velocity of the n-phase;

v_n- the vertical speed component of the n-phase;

f_n- the concentration (the volume content) of the n-phase;

 p-the pressure;

μ_n- the viscosity factor of the n-phase;

K- the interaction factor between the phases;

X_n, Y_n – the components of the body force of the n-phase;

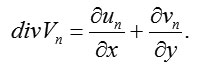
Here we investigate the stable one-dimensional flow of an ideal biphasic medium in open channels. We consider that both components are incondensable and that the body force may be ignored. Thus, the equation of motion for the considered case is as follows

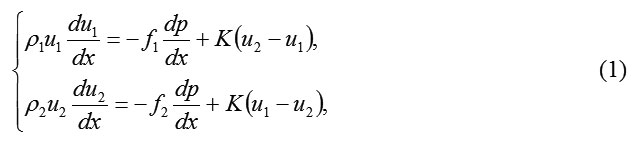
and the equation of continuity by virtue of the uniformity of discharge and in accordance with the discharge formulae is as follows:

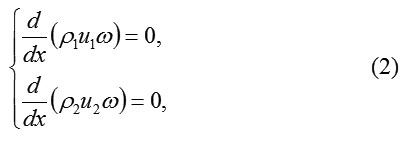
where ω is a cross-sectional area.

The systems (1) and (2) can be given as follows:

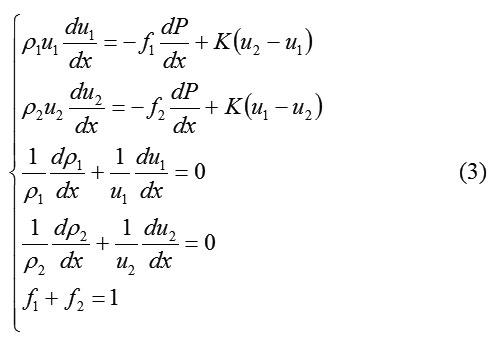
Thus, the system (3) is represented by

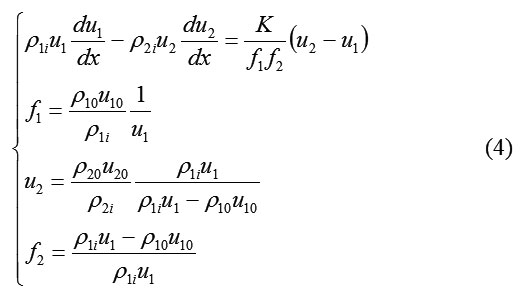
After the replacement of the three simultaneous equations given in Eq. (4), the first equation of this system and the simple transformation is given as follows:

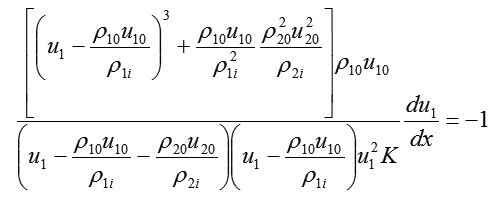
By integrating this equation at the primary condition in terms of x = x₀ and , we obtain the following for the speed of the primary components:

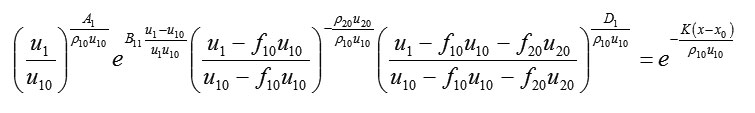
In the same way, for the speed of the second component:

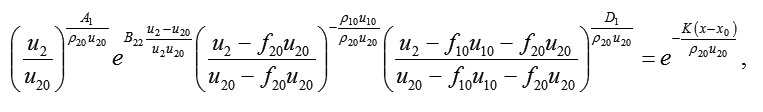
where

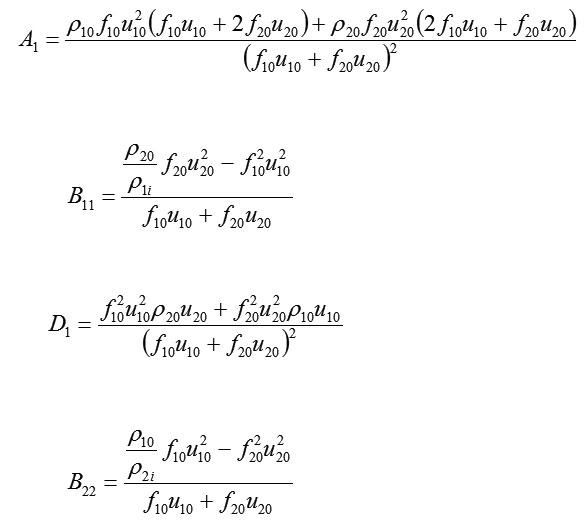
For concentration of the first and second components:

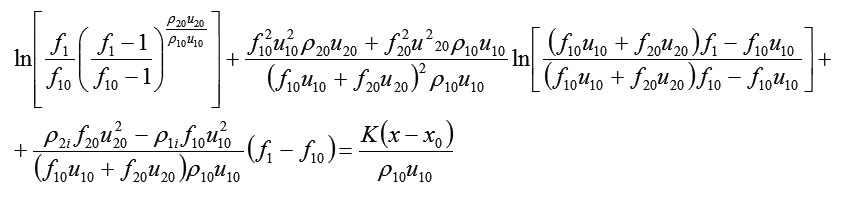
Having investigated these formulae, we can draw the following conclusions:

The motion of the two-component medium in terms of the speed of both components, according to the removal from the beginning of the movement, strives to be the same constant number f₁₀u₁₀ + f₂₀u₂₀ . The speed of the components with a faster primary speed remains more than this number, whereas the speed of the components with a slower primary speed is always lower. The speed of the components with a larger density f₁₀u₁₀ + f₂₀u₂₀  strives to be slower than the speed of the components with a smaller density. Thus, the concentrations of the components, in this regard, strive to various constant numbers.

References

1. Abalyants S. K. Stable and transient modes in the artificial channels.1981, Hydrometeoizdat, 267.
2. Nigmatullin R. I. The dynamics of the multiphase medium. Part 1,2. 1987, Nauka, 464.
3. Nyssanov Y. A. Theory and calculation of the interaction of the open flow and soil moistening. 2005, Reports of the National Academy of Sciences of the Republic of Kazakhstan 6, 89–93.
4. Umarov A. I., Akhmedov S. K. Bidimensional problems of the hydrodynamics of the multiphase medium. 1989, Tashkent: FAN, 96.