Department of Electrical, Electronic and Information Engineering, Faculty of Engineering Science, Kansai University, Osaka, Japan
DOI : https://dx.doi.org/10.13005/bpj/2241
Abstract
We investigated the dispersion characteristics of the propagation modes that progress on the tectorial membrane (TM). Recent studies have uncovered complex TM behavior and a possibility that TM might play an important role in the hearing system. An interaction between the TM and the fluid induces propagation modes, which are called TM modes. We found that there are several kinds of TM modes and analyzed the direction of the displacement of the TM that is caused by each mode. We also investigated the structural dependency of the angular wavenumber of each mode.
Keywords
Dispersion Relation; Mode Analysis; Propagation Mode; Tectorial Membrane
Download this article as:| Copy the following to cite this article: Kitamura T. Mode Analysis of Tectorial Membrane in Cochlea. Biomed Pharmacol J 2021;14(3). |
| Copy the following to cite this URL: Kitamura T. Mode Analysis of Tectorial Membrane in Cochlea. Biomed Pharmacol J 2021;14(3). Available from: https://bit.ly/3urMRDQ |
Introduction
The mammalian hearing system has high frequency selectivity and the cochlea responses are extremely tuned in the frequency domain. The cochlea is divided by the basilar membrane (BM) and Reissner’s membrane into three regions, which are called the scala vestibuli, scala media, and scala tympani. An interaction between the BM and the fluid elicits a slow wave mode, which is called BM mode, from the base to the apex in the cochlea. The BM mode is distributed in the vicinity of the BM and mainly contributes to the displacement of the BM1. The amplitude of the BM mode is amplified by active processes with the organ of Corti. Although many analytical and numerical models have been developed to clarify the cochlea hydrodynamics and the mechanics of the vibration of the BM2-6, it is still difficult to explain the high frequency selectivity of the cochlea only by this process.
The TM is overlying the surface of the organ of Corti and attaches along its medial side to the surface of the spiral limbus. It stretches across the spiral sulcus and attaches to the tips of the sensory hair bundles of the outer hair cells. An interaction between the TM and the fluid also induces propagation modes, which are called TM modes. TM was once thought to act merely as a stiff beam pivoting around its attachment point to the spiral limbus and generating the shearing motion between the surface of the organ of Corti and TM in response to the sound-induced vibrations of the BM driving the hair bundles7.
However, recent studies have uncovered more complex TM behavior and an ability to propagate travelling waves at audio frequencies along its length8-13. Zwislicki has hypothesized that the TM acts as a second resonator couple to the BM through the outer-hair-cell hair-bundle linkage. He has suggested that the cross-sectional structure of the cochlea partition is made up of two sets of distributed resonators, one consisting essentially of the distributed mass of the organ of Corti supported by the stiffness of the BM, and the other of the TM mass and its elastic attachment to the spiral limbus14. Ghaffari et al. have shown that the Tectb mutation reduces the spatial extent and propagation velocity of TM traveling waves and that these changes in wave propagation are likely to account for all of the hearing abnormalities associated with the mutation. They have stated that the Tectb mutation decreases the spread of excitation and increases frequency selectivity and that the change in TM wave velocity reduces the number of hair cells that effectively couple energy to the BM, which reduces sensitivity15.
The characteristics of wave propagation in TM highly depend on the structural parameters of TM such as the dimensions and Young’s modulus. Recent experimental studies have investigated the structural and mechanical properties of TM. Gueta et al. have characterized the mechanical properties of TM in the radial and longitudinal directions using nano- and microindentation experiments conducted using atomic force spectroscopy. They have shown that the stiffness in the main body of the TM and in the spiral limbus attachment zone does not change significantly along the length of the cochlea, while in contrast, the stiffness of the TM in the region above the outer hair cells increases by an order of magnitude in the longitudinal direction16. Richter et al. have shown using gerbil hemicochlea that a TM stiffness gradient exists along the cochlea similar to that of the BM. They have suggested that the changes in TM dimensions and the radial stiffness from base to apex would be able to provide a second frequency-place map in the cochlea17. Jones et al. have shown through mechanical measurements of isolated segments of TM that the stiffness of TM is reduced when it is mechanically stimulated at physiologically relevant magnitudes and at frequencies below their frequency place in the cochlea. They have also shown that the reduction in stiffness functionally uncouples the TM from the organ of Corti and minimizes energy loss during passive traveling wave propagation. Hayashi et al. have shown the remarkable gradient structure and molecular organization of the human TM by ultrastructural analysis and confocal immunohistochemistry 18.
In this study, we investigated the dispersion relations of the propagation modes that occur from an interaction between the TM and the fluid (TM modes). In a previous study, we investigated the coupling between TM mode and BM mode using a TM model that has a simple rectangular shape19. However, TM has a more complex shape that consists of the main body and the limbal attachment zone. Mode analysis of TM that has such a realistic shape has rarely been done. In this work, we focus on how the structural parameters affect the propagation characteristics by using mode analysis. First, we reviewed the studies that have shown the dimensions and Young’s modulus of TM and clarified the values. It is found that there are several kinds of TM modes and clarified the amplitude and direction of the displacement of the TM that is caused by each mode. We also investigated the structural dependency of the angular wavenumber of each mode. We used COMSOL Multiphysics software based on the finite element method (FEM) to analyze the effect of the elastic-wave mode.
Materials and Methods
Structural parameters of TM
Here, we review the recent studies that have investigated the structural and mechanical properties of TM. The basic structure of TM is shown in Fig. 1. According to Hayashi et al., the width w of the human TM increases from 68 μm (the hook region) to 186 μm (the upper middle region) along the cochlea. Similarly, the thickness h increases from 19 μm (the hook region) to 64 μm (the upper middle region)20. Gueta et al. have shown that the Young’s modulus of the TM of mice differs depending on the radial zone of TM. In the stiffness zone, it decreases from about 210 kPa (the basal region) to about 24 kPa (the apical region) along the cochlea16. Richter et al. have shown that the Young’s modulus of the TM of gerbil hemicochlea decreases from about 3 kPa (the basal region) to about 0.32 kPa (the apical region) along the cochlea17.
Analysis model
The human cochlea has about 35 mm length and coiled in a spiral of 2 1/2 to 2 3/4 turns. It is a triple-chambered fluid-filled duct, which is composed of the scala vestibuli, scala media, and scala tympani. TM lies over the surface of the organ of Corti which is in the scala media and spirals along the entire length of the cochlea. We modeled the cochlea as an uncoiled duct that has only TM. To limit our focus to the TM modes, we did not include the other parts of the organ of Corti, the BM, or the Reissner’s membrane in the analysis model. We conducted mode analysis to investigate the dispersion characteristics. TM is firmly attached to the spiral limbus and we modeled it as the rigid wall shown in Fig. 1. We assumed the lengths a = 10 μm and b = 50 μm and the length of the rigid wall d =30 μm. The width w and thickness h of the main body of TM are parameters. We assumed here that the height and width of the chamber are equally L. In accordance with the discussion in the previous section, we investigated the structural dependency of the angular wave number of TM modes in the following ranges: width w from 60 μm to 210 μm, thickness h from 20 μm to 70 μm, Young’s modulus E from 0.2 kPa to 220 kPa, and height L of the chamber from 0.5 mm to 4 mm. We fixed the ratio between the width and thickness of TM to w = 3 h for simplicity. The viscosity and damping of the fluid are not included. The density and bulk modulus of the fluid were 1.034×103 kg/m3 and 2.2×109 Pa, and the density and Poisson’s ratio of TM were 1.2×103 kg/m3 and 0.49, respectively21,22.
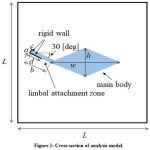 |
Figure 1: Cross section of analysis model. |
Results and Discussion
The results of the mode analysis revealed that there were several kinds of TM modes. Figures 2 and 3 illustrate the displacement of the TM of each mode when f = 2000 Hz and f = 10000 Hz, respectively. The displacement of mode 1, which had the lowest angular wave number, occurred all over the TM regardless of the frequency. The displacement of mode 2 was mainly on the limbal attachment zone of the TM when f = 10000 Hz, as shown in Fig. 3(b). On the other hand, we can see in Fig. 3(c) that the displacement of mode 3 was concentrated on the tip of the main body of TM when f = 10000 Hz. In either mode, the displacement spread to the other parts of TM when the frequency became lower, as shown in Fig. 2(b) and (c).
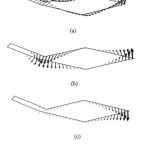 |
Figure 2: TM displacement of (a) mode 1, (b) mode 2, and (c) mode 3 when f =2000 Hz. |
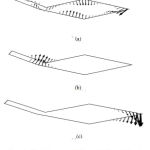 |
Figure 3: TM displacement of (a) mode 1, (b) mode 2, and (c) mode 3 when f = 10000 Hz. |
The dispersion diagrams of the TM modes ((a) mode 1, (b) modes 2 and 3) are shown in Fig. 4. As we can see, mode 1 had considerably smaller angular wave numbers k than the other two modes, and we therefore consider it to be a fast wave mode. In contrast, modes 2 and 3 correspond to slow wave modes. We can see from Fig. 4(b) that the two curves crossed around 3500 Hz. The displacement of TM started to concentrate on the limbal attachment zone (mode 2) or the tip of the main body (mode 3) above this frequency.
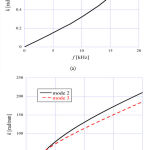 |
Figure 4: Dispersion diagram of (a) mode 1 and (b) modes 2 and 3. |
Figure 5 shows the angular wavenumber of the TM modes ((a) mode 1, (b) modes 2 and 3) as a function of the thickness h of TM, when f = 2000 Hz and 10,000 Hz. Here, we fixed the ratio between the width and thickness of TM to w = 3 h. As shown in Fig. 5(a), as the size of the TM main body got larger, the angular wavenumber of mode 1 monotonously increased, which means the decrease of the acoustic-wave velocity. On the other hand, we can see from Fig. 5(b) that the angular wavenumber of mode 3 decreased as the size of the TM main body became larger, while the one of mode 2 hardly changed. Each mode field pattern differed and therefore the location of the field concentration varied according to the mode. We conclude that this affects the dependency of the angular wavenumber on the TM main body size.
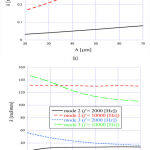 |
Figure 5: Angular wavenumber of (a) mode 1 and (b) modes 2 and 3 as a function of h when f = 2000 Hz and 10,000 Hz. |
Figure 6 shows the angular wavenumber of the TM modes ((a) mode 1, (b) modes 2 and 3) as a function of Young’s modulus E of the TM, when f = 2000 Hz and 10,000 Hz. It is understood that the angular wavenumber of every mode decreased as the Young’s modulus of the TM got larger. The acoustic-wave velocity is directly proportional to the square root of the Young’s modulus and therefore the angular wavenumber is presumed to be inversely proportional to the square root of the Young’s modulus of TM. As shown in Fig. 6 (b), mode 2 had a cutoff when f = 2000 Hz, and it didn’t even exist above about 45 kPa. We found that mode 3 also had a cutoff when the frequency was low and Young’s modulus was high.
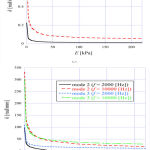 |
Figure 6: Angular wavenumber of (a) mode 1 and (b) modes 2 and 3 as a function of E when f = 2000 Hz and 10,000 Hz. |
Figure 7 shows the angular wavenumber of the TM modes ((a) mode 1, (b) modes 2 and 3) as a function of the height L of the cochlea chamber, when f = 2000 Hz and 10,000 Hz. Here, we assumed the width of the chamber is equal to the height. We can see from Fig. 7(a) that the angular wavenumber of mode 1 strongly depended on the size of the chamber. This is presumably due to the mode field having spread across the chamber. In contrast, we can see from Fig. 7(b) that modes 2 and 3 had a weak dependency of the angular wavenumber on the size of the chamber, although the angular wavenumber of mode 3 changed to some extent when L was less than 1.5 mm.
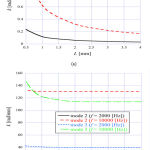 |
Figure 7: Angular wavenumber of (a) mode 1 and (b) modes 2 and 3 as a function of L when f = 2000 Hz and 10,000 Hz. |
Conclusion
We investigated the dispersion characteristics of TM modes, which occur from an interaction between the TM and the fluid. We showed that there are several kinds of TM modes and analyzed the direction of the displacement of the TM that is caused by each mode. We also investigated the dependency of the angular wavenumber of each mode on the size of the TM main body, Young’s modulus of the TM and the size of the cochlea chamber.
Conflict of Interest
The author do not have any conflict of interest.
Funding Source
This work did not receive any funding.
References
- Kitamura T. Investigation of coupling efficiency of slow-wave propagation mode along cochlea. Phys. Wave Phenom., 2019; 27: 242–245.
CrossRef - Parthasarathi A. A., Grosh K. and Nuttall A. L. Three-dimensional numerical modeling for global cochlear dynamics. J. Acoust. Soc. Am., 2000; 107: 474–485.
CrossRef - Neely S. T. Finite difference solution of a two-dimensional mathematical model of the cochlea. J. Acoust. Soc. Am., 1981; 69: 1386–1393.
CrossRef - Chan W. X. and Yoon Y. J. Effects of basilar membrane arch and radial tension on the travelling wave in gerbil cochlea. Hear. Res., 2015; 327: 136–142.
CrossRef - Elliott S. J., Ni G., Mace B. R. and Lineton B. A wave finite element analysis of the passive cochlea. J. Acoust. Soc. Am., 2013; 133: 1535–1545.
CrossRef - Ni G. and Elliot S. J. Comparing methods of modeling near field fluid coupling in the cochlea. J. Acoust. Soc. Am., 2015; 137: 1309–1317.
CrossRef - Jones G. P., Lukashkina V. A., Russell I, J., Elliott S. J. and Lukashkin A. N. Frequency-dependent properties of the tectorial membrane facilitate energy transmission and amplification in the cochlea. Biophys. J., 2013; 104: 1357–1366.
CrossRef - Ghaffari R., Aranyosi A. J., Richardson G. P. and Freeman D. M. Tectorial membrane travelling waves underlie abnormal hearing in Tectb mutant mice. Nat. Commun., 2010; 1:96 doi: 10.1038/ncomms1094.
CrossRef - Russell I. J., Legan P. K., Lukashkina V. A., Lukashkin A. N., Goodyear R. J. and Richardson G. P. Sharpened cochlear tuning in a mouse with a genetically modified tectorial membrane. Nat. Neurosci., 2007; 10: 215–223.
CrossRef - Gummer A. W., Hemmert W. and Zenner H. P. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc. Natl. Acad. Sci. USA, 1996; 93: 8727–8732.
CrossRef - Chadwick R. S., Dimitriadis E. K. and Iwasa K. H. Active control of waves in a cochlear model with subpartitions. Proc. Natl. Acad. Sci. USA, 1996; 93: 2564–2569.
CrossRef - Meaud J. and K. Grosh K. The effect of tectorial membrane and basilar membrane longitudinal coupling in cochlear mechanics. J. Acoust. Soc. Am., 2010; 127, 1411–1421.
CrossRef - Sellon J. B., Ghaffari R. and Freeman D. M. Geometric requirements for tectorial membrane traveling waves in the presence of cochlear loads. Biophys. J., 2017; 112: 1059–1062.
CrossRef - Zwislocki J. J. Analysis of cochlear mechanics. Hear. Res., 1986; 22: 155–169.
CrossRef - Ghaffari R., Aranyosi A. J. and Freeman D. M. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Natl. Acad. Sci. USA, 2007; 104: 16510–16515.
CrossRef - Gueta R., Barlam D., Shneck R. Z. and I. Rousso I. Measurement of the mechanical properties of isolated tectorial membrane using atomic force microscopy. Proc. Natl. Acad. Sci. USA, 2006; 103: 14790–14795.
CrossRef - Richter C. P., Emadi G., Getnick G., Quesnel A. and Dallos P. Tectorial membrane stiffness gradients. Biophys. J., 2007; 93: 2265–2276.
CrossRef - Jones G. P., Lukashkina V. A., Russell I. J., Elliot S. J. and Lukashkin A. N. Frequency-dependent properties of the tectorial membrane facilitate energy transmission and amplification in the cochlea. Biophys. J., 2013; 104: 1357–1366.
CrossRef - Kitamura T. and Horii Y. Investigation on coupling between tectorial membrane mode and basilar membrane mode along cochlea. Biomed. Res., 2020; 31: 199–202.
- Hayashi H., Fischer A. S., Glueckert R., Liu W., Salvenmoser W., Santi P. and Andersen H. R. Molecular organization and fine structure of the human tectorial membrane: is it replenished? Cell Tissue Res., 2015; doi: 10.1007/s00441-015-2225-5.
CrossRef - Koike T., Sakamoto C., Sakashita T., Hayashi K., Kanzaki S. and Ogawa K. Effects of a perilymphatic fistula on the passive vibration response of the basilar membrane. Hear. Res., 2012; 283: 117–125.
CrossRef - Paolis A. D., Bikson M., Nelson J. T., Alexander de Ru J., Packer M. and Cardoso L. Analytical and numerical modeling of the hearing system: advances towards the assessment of hearing damage. Hear. Res., 2017; 349: 111–128.
CrossRef








