Nidhi Katiyar¹, Ravindra Nath²  and  Shashwat Katiyar³

Dr. APJ Abdul Kalam Technical University (AKTU), Lucknow.

University Institute of Engineering, Technology, CSJM University, Kanpur, U.P., 208024, India.

Institute of Bioscience and Biotechnology, CSJM University, Kanpur, U.P., 208024, India.

Corresponding Author E-mail : nidhi26kanpur@gmail.com 

DOI : https://dx.doi.org/10.13005/bpj/2259

Abstract

Dengue is the pandemic disease caused by Dengue virus (DENV), a mosquito-borne flavivirus. In recent years dengue has emerged as a foremost cause of severe illness and deaths in developing countries.About  400 million dengue infections occur worldwide each year.In general, dengue infections create only mild illness but infrequently expand into a  lethal illness termed as severe dengue for which no specific treatment. The machine learning approach plays a significant role in bioinformatics and other fields of computer science.It exploitsapproaches like Hidden Markov Model (HMM), Genetic Algorithm (GA), Artificial Neural Network (ANN), and Support Vector Machine (SVM).The GA is a randomized search algorithm for solving the problem based on natural selection phenomena.Many machine learning techniques are based on HMM have been positively applied. In this work, We firstly used HMM parameters on the biological sequence,and after that, we catch the probability of the observation sequence of a mutated gene sequence. This study comparesboth methods, G.A. and HMM, to get the highest estimated value of the observation sequence. In this paper, we also discuss the applications ofGA in the bioinformatics field. In a further study, we will apply the other machine learning approaches to find the best result of protein studies.

Keywords

Artificial Neural Network; Dengue; Evolutionary Algorithm; Flavivirus Genetic Algorithm; Hidden Markov model; Methyltransferase Protein; Machine Learning; Protein Data bank

Download this article as: 

Copy the following to cite this article: Katiyar N, Nath R, Katiyar S. Genetic Algorithm Approach to Find the Estimated Value of HMM parameters for NS5 Methyltransferase Protein. Biomed Pharmacol J 2021;14(3).

Copy the following to cite this URL: Katiyar N, Nath R, Katiyar S. Genetic Algorithm Approach to Find the Estimated Value of HMM parameters for NS5 Methyltransferase Protein. Biomed Pharmacol J 2021;14(3). Available from: https://bit.ly/2UaWclO

Introduction

Dengue virus (DV), the causative agent of dengue, resides in the family Flaviviridae and is transmitted to humans by biting Aedesaegypti mosquitoes. Four serotypes (Dengue Virus serotype 1, Dengue virus serotype 2, Dengue virus serotype 3, and Dengue virus serotype 4) are recognized (El Sahili, Lescar2017).The range of dengue disease spans from a flu-like disease termed dengue fever to Dengue hemorrhagic fever. In chronic cases, it causes dengue shock syndrome and sometimes terminates in death. The most prevalent clinical symptoms of acute dengue disease are hemorrhagic diathesis, liver involvement, and plasma leakage.The DV genome is prepared into a single open reading frame (ORF)of single-stranded (positive -sense) RNA of 900 kDa and flanked at 5’end by type I cap and at 3’end by untranslated regions and encodes a precursor polyprotein. Post-translational modification of precursor protein gives rise to three structural (C, prM, and E) proteins and seven non-structural(NS1, NS2A, NS2B, NS3, NS4A, NS4B, and NS5)proteins(Anasiret al.,2020).

The NS5, non-structural methyltransferase, is the largest and conserved region of the genome among all serotypes. It is a bifunctional enzyme with a Methyltransferase domain (MTase; residues 1–296) at its N-terminal end and anRNA-dependent RNA polymerase (RdRp; residues 320–900) at its C-terminal end (Vannice2016).This protein has three active sites, namely S-adenosylmethionine(SAM)S-adenosyl-homocysteine (SAH), guanosine triphosphate (GTP), and RNA-binding site (Herreroet al., 2013).

In this work, we considerthe NS5 Methyltransferase protein of the Dengue Virus to find out the probability of observation sequence. Firstly we convert the protein sequence into nucleotide sequence. After that, we implement the G.A. (selection, crossover, and mutation operator).The forward algorithm of HMM is already well discussed in my previous paper (Katiyaret al., 2020) to calculate the probability of the observation sequence. In their work, we compare both (HMM and GA) results in the bases of crystallography data the resolution (in Angstroms).

Here, we define the Hidden Markov Model as probabilistic models, in which sequences are generated from two simultaneous stochastic processes.This model captures the hidden information from observable sequential symbols (e.g., a nucleotide sequence AGCT).This model is defined by states (n), state probabilities (m), transition probabilities (a), emission probabilities (b), and initial probabilities (i). Therefore in a hidden model, there are two stochastic processes: moving between states and the process of emitting an output sequence. The sequence of state transitions is a hidden process and is observed through the sequence of emitted symbols(Alghamdi R 2016).

HMM is characterized by the following:

N – The number of states in the model.

M- The number of district observation symbols per state.

The state transition probability distribution A = (a_ij)

The observation symbol probability distribution B = {b_j(k)}

The initial state distribution π =  (π_i)

Given applicable values of N, M, A, B, and π, the HMM can be used as a maker to give an observation sequence.

Three Basic Problems for HMM^s

Given the form of HMM of the previous section, there are three basic problems of interest that must be solved for the model to be useful in real-world applications (Mor Bet al., 2020).

These problems are the following:

Problem 1: Given the observation sequence O = O¹ O²…… O^.T. and a model  λ = (A, B, π), how do we efficiently compute P (O| λ), the probability of the observation sequence, given the model?

Problem 2: Given the observation sequence O = O¹ O²……O^T and the model  λ, how do we choose a corresponding state sequence Q = q¹, q²………. q^T, which is optimal in some meaningful sense (i.e., best “explains” the observations)?

Problem 3: How do we adjust the model parameters  λ = (A, B, π) to maximize P (O| λ)?

Genetic Algorithm (GA)

The genetic algorithm is a method of natural selection that belongs to the class of Evolutionary Algorithms (EA).Genetic Algorithms type of optimization algorithm, meaning they are used to find the optimal solution(s) for a given problem that maximizes or minimizes solution of problem(Silvaet al., 2019).A Genetic Algorithm is the biological process of reproduction and natural random selection to find for the best `fittest’ solution. Like evolution, several of a genetic algorithm’s works randomly permit us to set the level of randomization and control (Jenningset al. 2019). These are expected to be more powerful algorithms providing random and in-depth search. Such features prove GA to be better than other optimization methods, which have drawbacks like lack of stability, derivatives, linearity, or other features. GAareoften designed to simulate a biological process.However, the entities that this terminology refers to in genetic algorithms much simpler than their biological complements (L Halduraiet al., 2016).

The basic components of Genetic Algorithms are:

Function of optimization

Population of chromosomes

Random selection of chromosomes

Crossover to next generation of chromosomes

Mutation of chromosomes in the new generation

Some programming languages are also used to implement the GA. They are also well suited for modeling occurrences in economics, ecology, the human immune system, population genetics, and social systems optimization, machine learning optimization (Harsh Bhasinet al. 2011) etc.

The necessary steps involved in the genetic algorithm are (i) generate a random population (suitable and possible solutions for the problem) of chromosomes, (ii) calculate the fitness f(x) of each chromosome (x), (iii) repeat the process until a totallynew population is created, (iv) select two parent chromosomes of better fitness, (v) taking into consideration of crossover probability, a crossover is performed between the selected parents (without crossover offspring would be same as a parent), (iv) similarly, with some mutation probability, the new offspring is mutated at each locus, (vii) resulting new offspring is placed in a new population, (viii) the newly generated population is used for running with the genetic algorithm, (ix) if end condition is satisfied, run is stopped, the resultant best solution is placed in the current population and (x) go back to step number two for its fitness evaluation.

A list of some genetic algorithm applications is shown in (Table 1). GA methods play a significant role and provide a useful set of tools in different fields and bioinformatics analysis.

Table 1: Some common applications of Genetic Algorithm

Domain	Application Type
Business	Control the gas pipeline, missile evasion
Optimization	Molecular structure optimization, Data compression system,  stochastic optimization
Management and Engineering	Computer-automated design, vehicle routing problem, sorting network, quality control
Design	Power, electronics aircraft design, keyboard configuration,communication network
Robotics	Trajectory planning
Machine Learning	Learning fuzzy rule base using genetic algorithms, neural networks
Game Playing	Poker, checkers
Security	Encryption, Decryption, and code-breaking
Image Processing	Dense pixel matching
Bioinformatics	Multiple sequence alignment, motif discovery, building phylogenetic trees, protein folding, and protein/ligand docking
Other Applications	Multidimensional system, mutation testing, wireless sensor networks, and clustering using a genetic algorithm.

The GA-based methodology provides accuracy, efficiency, and potential for growth to data analysis in bioinformatics. The basic principle behind GAs is that itcreates and maintains a population of individuals represented by chromosomes. Chromosomes are essentially a character string analogous to the chromosomes appearing in DNA. These chromosomes are typically encoded solutions to a problem, which then undergo a process of evolution according to rules of reproduction and mutation.

Material and methods

In this work, we use the NS5 Methyltransferase protein sequence. The protein structure was downloaded from RCSB PDB (http://www .rcsb.org), and accession codes are used in this study. The coordinates and structure factors for DENV-2 NS5  Methyltransferase protein complexes have been deposited in the Protein Data Bank under accession code.

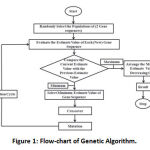Figure 1: Flow-chart of Genetic Algorithm. Click here to view figure

Find the optimization value of the function. In the process of the crossover method, first, we select any one population and select any two random points of some length shown in (Figure 1). The same process can be done in the second selected population Then we exchange that portion from one population to the other. In mutation, we make minor changes in anyone’s population. Now find the estimated values of both population and compare these estimated values with previously estimated values and check which will be better estimate value. At last, select the population contains a better-estimated value.

Table 2: List of the dengue NS5 methyltransferase proteins with resolution power.

S. No	Pdb code	Resolution Power	Residues Count	References
1.	2P1D	2.90 Å	305	Egloff, M.P., Benarroch, D.   (2002)
2.	2P3O	2.76 Å	305	Egloff, M.P., Decroly, E.       (2007)
3.	2P3Q	2.75 Å	305	Egloff, M.P., Decroly, E.       (2007)
4.	2P40	2.70 Å	305	Egloff, M.P., Decroly, E.       (2007)
5.	1R6A	2.60 Å	295	Benarroch, D., Egloff            (2004)
6.	1L9K	2.40 Å	305	Egloff, M.P., Benarroch, D.   (2002)
7.	4V0Q	2.30 Å	892	Zhao, Y., Soh, S., Zheng,       (2015)
8.	3EVG	2.20 Å	275	Geiss, B.J., Thompson           (2009)
9.	2P3L	2.20 Å	305	Egloff, M.P., Decroly, E.       (2007)
10.	5EIF	2.00 Å	552	Benmansour, F., Trist, I.        (2016)
11.	4R05	2.00 Å	534	Brecher, M.B., Li, Z.             (2015)
12.	3MTE	1.80 Å	444	Macmaster, R., Zelinskaya, N. (2010)
13.	2P41	1.80 Å	305	Egloff, M.P., Decroly, E.     (2007)
14.	5E9Q	1.79 Å	512	Benmansour, F., Trist, I.     (2016)
15.	3P8Z	1.79 Å	534	Lim, S.P., Sonntag, L.S.      (2011)
16.	5EC8	1.76 Å	552	Benmansour, F., Trist, I.     (2016)
17.	5EKX	1.76 Å	552	Benmansour, F., Trist, I.     (2016)
18.	3P97	1.74 Å	534	Lim, S.P., Sonntag, L.S.      (2011)
19.	5CUQ	1.74 Å	534	Brecher, M., Chen, H.         (2015)
20.	3MQ2	1.69 Å	436	Macmaster, R., Zelinskaya, N. (2010)

Implementation of HMM using GA

In the implementation of the Genetic algorithm, we have taken the state transition matrix used in the forward algorithm of the HMM (as described inmy previous paper published) (Katiyaret al., 2020). (Table 2) shows the data of 20 gene sequences of non-structural methyltransferase protein with resolution power, their number of residues count and relevant references.

Selection of Population

From (Table 2), we select any two sequences, i.e. (PDB code1 and PDB code2), as the initial population and apply the crossover and mutation function and generate the estimated values of both populations using the forward algorithm of HMM. Then select the population PDB code of better-estimated value. Again we select the one sequence of PDB code from (Table 2) and other PDB code, which contains a better-estimated value and applies the same crossover and mutation function now. Once again, find which PDB code contains a better estimate value; this process will continue until all the PDB code finished from the (Table 2).

Crossover

To generate a random population, we applied the crossover operator on the given gene sequences. In this method, we have selected the two gene sequences (among 1 to 20 protein codes in table 2) of NS5 Methyltransferase protein of dengue virus and interchanged their position.

Mutation

In this process, we slightly changed a small part of the gene sequence. In a simple sentence, we can say that mutation would change one or more genes, also called as interchanging mutation. After applying the mutation operator, we get the mutated gene sequence, and after this, we calculate the optimum value of the gene sequence of using the forward method of the HMM approach.

In this method, we used the two strings of gene sequences of NS5 methyltransferase protein then applied the crossover and mutation operator. Further,the process of selection, crossover, and mutation operator was performedshown in (Figure 2).

Figure 2: Selection, Crossover, and Mutation operator Applied. Click here to view figure

Selected two points randomly of some length in seq1, and the same length at seq2 then applied the crossover operation. In crossover operation, exchange the selected part from both gene sequence seq1 and seq2, and at the result, we have got seq1* and seq2*; and after this, we did mutation operator seq2* and got the seq2**. (In mutation operation here, we have selected a single char ‘G’ and char ‘C’ at the different places of seq2* and then interchange both characters, and get the seq2**).The same process is applied in the (Figure 3). In which we have got results after crossover and mutation operation.

Figure 3: Result of after mutation operation. Click here to view figure

Following matrix for the forward algorithm of HMMs, where each sequence have individual tables ofA = (a_ij), B = {b_j(k)} and π =  (π_i) matrix values.

Table 3 Click here to view table

Using matrices of A, B, and Pi, we apply the GA and forward algorithm of HMM to find the global maxima value of P(O| λ) and store in (Table 4).

Table  4: Showing the value of P(O| λ)using the Forward Algorithm and Genetic Algorithm.

S. No	Gene Sequence after mutation	Residues Count	P(O| λ) value after Forward Algorithm	P(O| λ) value after Genetic Algorithm
1.	5EIF	980	3.96E-278	1.63E-266
2.	5EC8	980	3.50E-282	1.78E-276
3.	5E9Q	902	8.93E-269	1.08E-244
4.	5CUQ	936	1.85E-259	9.86E-271
5.	4VOQ	1625	0.00E+00	0.00E+00
6.	4R05	936	8.06E-270	3.31E-266
7.	3P97	936	8.59E-280	1.76E-272
8.	3P8Z	936	1.16E-279	8.39E-274
9.	3MTE	755	1.40E-210	5.51E-206
10.	3MQ2	740	3.48E-213	1.81E-206
11.	1R6A	514	6.86E-300	2.86E-284
12.	1L9K	530	1.96E-304	1.87E-306
13.	2P1D	530	5.29E-321	9.35E-296
14.	3EVG	481	3.44E-281	3.34E-278
15.	2P3L	530	1.96E-304	1.99E-313
16.	2P3O	530	1.96E-304	1.20E-304
17.	2P3Q	530	1.88E-304	7.08E-311
18.	2P40	481	1.96E-304	8.83E-295
19.	2P41	530	1.96E-304	1.66E-307
20.	5EKX	980	1.15E-282	2.74E-274

Results and Discussion

This paper presents a comparative result of HMM and GA with the resolution power (crystallographic value of protein sequence given in Table 2).Table3 shows the value of P(O| λ) for the gene sequences taken in this research work after the crossover and mutation operation of the GA and forward algorithm of HMM. The result also depends on the length of the gene sequence. We have taken 20 gene sequences of NS5methyltransferase protein with residues count (i.e.,the total number of A, G, C, and T characters in sequence) and P (O| λ) value of the forward algorithm of HMM and P (O| λ) of the value of forwarding algorithm after applying GA method. We observed that sequences that have the minimum values of protein 3MTE are1.40E^-210,and the maximum value of protein 1L9K is 1.96E^-304 in the forwarding algorithm. But after GA protein code 2P3Q has the minimum value 7.08E^-311 while the maximum values of protein 3MQ2 is1.81E^-206. Using Table 3, we are comparing and showing the value after the forward algorithm and after GA in (Figure4).

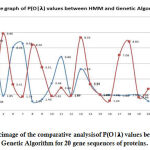Figure 4: Graphicimage of the comparative analysisof P(O|𝛌) values between HMM and Genetic Algorithm for 20 gene sequences of proteins. Click here to view figure

(Figure4) shown thecomparative graph of between HMM and GA to find which method shows the global maxima. Here we observed that in GA, global maxima values lie between (9.85 to 9.35) while in HMM, global maxima values lie between (8.93 to 8.59).So we can say for this experiment, the values of GA for global maxima always give a better result as compared to the HMM forward algorithm. So, here we can state that we can use the global maximum values of both the algorithms so as to get the knowledge of which protein to use among the given four protein as a drug target (in case of drug design). Thus, we obtained the better protein in all four proteins which have maxima values, can take any protein which has the highest value of, i.e., (9.86).

In the case study, we discussed the crystallographic data of the resolution (in Angstroms) of a protein structure resolved by X-ray diffraction or Nuclear Magnetic Resonance (NMR). This field can be queried for a value or a range of values. But here, we apply the computational methods to find the resolution power of a protein sequence to take the large data of protein sequence.Most of the structure data are obtained from X-ray crystallography and NMR-spectroscopy. X-ray crystallography determines the preparation of atoms within a protein by passing X-rays through a crystallized form of the protein and analyzing the resulting X-ray diffraction pattern. This technique provides the highest resolution and usually yields only one model of a structure. Nuclear magnetic resonance (NMR) determines the structure of a protein in solution and generally yields multiple models, which allow for a description of the biomolecule’s signaling solution(Madej T, Lanczycki CJ  et al., 2014).In addition to these experimental methods, some researchers use computational modeling to predict the structure of a protein by simulating the forces that act on each atom in a molecule of known structure. However, this method produces non-experimental models and the least dependable results.

Conclusion

In this work, we are studying and applying the GA and forward algorithm of HMM on the protein sequence of NS5 Methyltransferase protein of the dengue virus. At last, we compared the estimated value of the forward algorithm of HMM with the GA approach. In our experiment, we observed that the genetic algorithm provides a better result as compared to the forward algorithm. In the future, we will repeat this experiment with a large number of gene sequences with higher lengths and will compare the results of different algorithms like GA, Metropolis, GWW, and Ant Colony algorithms to evaluate their capabilities to find the global maxima. In a further study, we will improve the algorithm and make it more effective for long protein sequence prediction using a multi-core computing platform used other machine learning approaches as an above mention for the biological data generation in the analysis and discovery for the drug design.

Acknowledgement

This study is part of Doctoral research work, and both authors read and approved the final manuscript.

Conflict of Interest

All the authors declare that there are no conflicts of interest regarding the publication of this research paper.

Funding Source

This work did not provide any source of financial support.

References

1. Anasir M IRamanathan B and Poh C L. Structure-Based Design of Antivirals against Envelope Glycoprotein of Dengue Virus Viruses., 2020; 12:4: 367.
   CrossRef
2. Amjad M K Butt S I Kousar R Ahmad Agha M H Faping Z Anjum N Asgher U. Recent Research Trends in Genetic Algorithm Based Flexible Job Shop Schedulling Problems Mathematical  Problems in Engineering Article ID 9270802., 2018; 32.
   CrossRef
3. Alghamdi R. Hidden Markov Models (HMMs) and security applications Int J AdvComputSci Appl., 2016; 7: 2: 39-47.
   CrossRef
4. Benmansour F Trist I Coutard B Decroly EQuerat G Brancale A and Barral K. Discovery of novel dengue virus NS5 methyltransferase non-nucleoside inhibitors by fragment-based drug design European journal of medicinal chemistry., 2017; 125: 865-880.
   CrossRef
5. Brecher M B Li Z Zhang J ChenH Lin Q Liu B and Li H. Refolding of a fully functional flavivirus methyltransferase revealed that S‐adenosyl methionine but not S‐adenosylhomocysteine is copurified with flavivirus methyltransferase Protein Science., 2015; 24: 1: 117-128.
   CrossRef
6. Chuang C H Chiou S J Cheng T L and Wang Y T. A molecular dynamics simulation study decodes the Zika virus NS5 methyltransferase bound to SAH and RNA analogue Scientific reports., 2018; 8: 1: 6336.
   CrossRef
7. El Sahili A and Lescar J. Dengue Virus Non-Structural Protein 5 Viruses., 2017; 9: 4: 91.
   CrossRef
8. Herrero L J et al. , 2013; 137: 266-82.
9. Harsh Bhasinet al.Application of Genetic Algorithms in Machine learning International Journal of Computer Science and Information Technologies (IJCSIT). , 2011; 2: 5: 2412-2415.
10. Jennings C Lysgaard S Hummelshøj JS et al.Genetic algorithms for computational materials discovery accelerated by machine learning npjComput Mater., 2019; 5: 46.
    CrossRef
11. Katiyar, Nidhi, Nath, Ravindra and Katiyar, Shashwat. Estimated Value of Hidden Markov Model Parameters for NS5 methyltransferase Protein of Dengue Virus.International Journal on Emerging Technologies., 2020; 11: 1: 01–11.
12. L Haldurai T Madhubala and R Rajalakshmi. A Study on Genetic Algorithms and its Applications In ternational Journal of Computer sciences and Engineering., 2016; 4: 10: 139-143.
13. Lim S P Sonntag L S Noble C Nilar S H Ng R H Zou G and Bodenreider C. Small molecule inhibitors that selectively block dengue virus methyltransferase Journal of Biological Chemistry., 2011; 286: 8: 6233-6240.
    CrossRef
14. Macmaster R Zelinskaya N Savic M Rankin C R and Conn G L. Structural insights into the function of aminoglycoside-resistance A1408 16S rRNA methyltransferases from antibiotic-producing and human pathogenic bacteria Nucleic acids research., 2010; 38: 21:7791-7799.
    CrossRef
15. Madej T Lanczycki CJ Zhang D Thiessen PA Geer RC Marchler-Bauer A Bryant SH. MMDB and VAST+:tracking structural similarities between macromolecular complexesNucleic Acids Res., 2014;42: 1:297-303.
    CrossRef
16. Mor B Garhwal S and Kumar A. A Systematic Review of Hidden Markov Models and Their Applications Arch Computational Methods Eng., 2020; https://doi.org/10.1007/s11831-020-09422-4.
    CrossRef
17. V. Chandrika, K. Visalakshmi and K. Sakthi Srinivasan Application of Hidden Markov Models in Stock Trading 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS) Coimbatore India., 1144-1147.
    CrossRef
18. Qiong C Huang M Xu Q Wang H Wang J. Reinforcement learning-Based Genetic Algorithm in Optimizing Multidimensional Data Discretizatio Scheme Mathematical Problems in Engineering., 2020; 13.
    CrossRef
19. Silva FT Silva MX and Belchior JC (2019). A New Genetic Algorithm Approach Applied to Atomic and Molecular Cluster Studies.
    CrossRef
20. S. F. Tambunan et al. Drug Target Insights., 2017; 1-11.
    CrossRef
21. VanniceKS Durbin AHombach J. Status of vaccine research and development of vaccines for dengueVaccine., 2016; 34: 2934–8.
    CrossRef
22. Yang Q M Yang Jack Y. Lecture notes and beyond the decade of high-performance computing for the next-generation sequence analysis I J Computational Biology and Drug Design., 2010; 2: 2: 204-206.
    CrossRef
23. Zhao Y Soh T S Zheng J Chan K W K Phoo W W Lee C C and Shi P Y. A crystal structure of the dengue virus NS5 protein reveals a novel inter-domain interface essential for protein flexibility and virus replication PLoS pathogens., 2015; 11: 3: 1-27.
    CrossRef
24. Zhou YH Brooks P Wang X. A two-stage Hidden Markov Model design for biomarker detection, with application to microbiome research Stat Biosci., 2018; 10: 1-18.
    CrossRef

(Visited 307 times, 1 visits today)