Sugandha Agarwal ¹, O.P. Singh¹ and Deepak Nagaria²

¹Amity School of Engineering and Technology, Amity University, Lucknow.

²Electronics and Communication Department, BIET, Jhansi.

Corresponding Author E-mail: sugandhaa7@gmail.com

DOI : https://dx.doi.org/10.13005/bpj/1174

Abstract

Medical imaging plays a dominant role in clinical practice like diagnosis, therapy, etc. and research related findings. Medical images are usually contaminated or distorted while acquiring and transmitting the image due to several types of noises, misfocus of camera, disturbance due to blood flow, atmospheric turbulence. So it becomes necessary to apply image denoising processing to improve the quality of image. The search for efficient image denoising methods is still a valid challenge at the crossing of functional analysis and statistics. This paper compares the efficiency of wavelet based thresholding techniques in the presence of speckle noise for various wavelet family i.e. Haar, Morlet, Symlet, Daubechies in denoising a medical imaging resonance of brain. Performance estimation and analysis is done using SNR (Signal to Noise Ratio), PSNR (Peak Signal to Noise Ratio) and MSE (Mean Square Error). Based on the performance evaluation, it is inferred that wavelet transform is more effective as it has an ability to capture the energy of a signal in a few energy transform values usually known as wavelet coefficients.

Keywords

Image denoising; Threshold; Wavelet transform; MRI; PSNR; and MSE

Download this article as: 

Copy the following to cite this article: Agarwal S, Singh O.P, Nagaria D. Analysis and Comparison of Wavelet Transforms for Denoising MRI Image. Biomed Pharmacol J 2017;10(2).

Copy the following to cite this URL: Agarwal S, Singh O.P, Nagaria D. Analysis and Comparison of Wavelet Transforms for Denoising MRI Image. Biomed Pharmacol J 2017;10(2). Available from: http://biomedpharmajournal.org/?p=15194

Introduction

With the revolution in contemporary medicines, medical imaging techniques such as magnetic resonance imaging (MRI), ultrasound, CT scan, etc. have been widely employed for more accurate and precise pathological variations as well as diagnosis. Medical imaging based diagnosis is noninvasive procedure thereby helping clinical practioner in better diagnosis and improving comfort to the patient. Of all the imaging techniques MRI based diagnosis is highly effective and promising. For the superlative diagnosis of internal anatomical features, it is imperative to obtain sharp, higher resolution and noise free image with the aid of digital image processing technique [1]. However medical imaging suffer number of inadequacies which includes noise from equipment while acquiring, ambient noise, noise due to background tissue, disturbance due to other organs and anatomical influences such as blood flow, body fat and breathing motion. Therefore removal of noise or disturbance from the medical images are essential, as noise limit the effectiveness of medical image diagnosis [2, 6]. Thus severely degrading the image quality and causing loss of image information details.

Conventionally image denoising is accomplished with the help of linear processing techniques such as wiener filtering, median filtering, Gaussian filtering, etc. [3, 4 and 5]. Sometimes while removing noise from the acquired image, blur is introduced [7]. In recent years, many researchers have applied wavelet thresholding and threshold selection based techniques for denoising image since wavelet thresholding offers a suitable basis for extracting noisy signal from the original image signal [8, 9]. The motivation of using wavelet transform for denoising MRI image that it provide good energy compaction, i.e. it has an ability to capture the energy of a signal in few energy transform values [10, 11].

Wavelets based transform are mathematical tools which are used to extract information from images [12]. A significant benefit it has over Fourier transforms is temporal resolution which signifies that it can captures both frequency and location information of the images [13]. Wavelets are localized in both time and frequency whereas the standard Fourier transform is only localized in frequency. Wavelet transforms are now being implemented replacing Fourier transform for numerous domains of image processing such as image retrieval[14, 15], medical imaging, image watermarking[17], image compression [22] and many more. For de-noising, medical images orthogonal wavelets with a wavelet function have played a dominant role [16, 18]. In recent years the wavelet transform based denoising has emerged as an alternative to formerly used Fourier Transform (FT) and its co-transforms, namely Discrete Sine Transform (DST) [18] and Discrete Cosine Transform (DCT) [19, 20]. Wavelet transform has exceptional localization property and also has capability of energy packet reduction [21].

With the increasing demand of de-noised image in all the day to day applications, introducing efficient image de- noising algorithm is still a challenge for researchers as noise removal introduces artifacts and causes blurring of the images. This paper elaborate different methodologies for denoising a brain MRI providing an insight as to which algorithm should be utilized for more reliable estimate of the original image using PSNR, SNR and MSE evaluation factors.

Wavelet Transform

Wavelet is interdisciplinary and implementing image denoising using wavelet transform is similar to the working of human eye. It was developed to allow some temporal or spatial information of the image. Wavelet are basically produced from one single function (basis function) called mother wavelet. The wavelet function work on an idea of using a family of functions localized in both time and frequency. It represents an image as a sum of wavelet functions with different locations and scales. Decomposition of an image into wavelets involves a high frequency waveforms containing detailed part of an image called wavelet function and low frequency waveform representing smooth part of the image called scaling function. Using wavelet transform, image can be decomposed at different levels of resolution as wavelet decomposition has varying window size and can also be processed from low resolution to high resolution as wavelet transformation is localized both in time and frequency domains.

When an image is decomposed using wavelet transform, it produces four sub images i.e. approximation details, horizontal details, vertical details and diagonal details in which there are two coefficients namely small coefficients and large coefficients. Small coefficients arises due to noise and can be thresholded without affecting the significant features of the image. Whereas large coefficients are generated due to essential signal features. In thresholding technique or non-linear technique only one wavelet coefficient is operated at a time. In thresholding technique, each coefficient is compared against generated threshold value. If the coefficient is smaller than threshold, then it is set to zero; otherwise it is kept or modified. After performing thresholding, inverse wavelet transform is performed to reconstruct essential image characteristics with lesser noise. When multilevel wavelet decomposition of image is performed we obtain sub bands LL2 (low frequency or approximation coefficients), HL2 (horizontal details), LH2 (vertical details), HH2 (diagonal details) and the first level details HL1, LH1, HH1 as shown in figure 1. Similarly higher level decomposition is also feasible using same procedure.

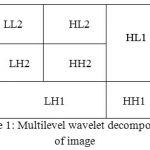Figure 1: Multilevel wavelet decomposition of image   Click here to View figure

For denoising MRI image selection of mother wavelet plays a dominant role. In wavelet transform family numerous types of wavelets such as Haar, Morlet, Symlet, Daubechies, etc. are available. Haar transform is the oldest and the simplest transform. It is discontinuous in nature just like step function. Haar is used to analyze images efficiently at various resolutions. Daubechies transform is the most popular transform it has lead the foundation of wavelet based multidimensional signal processing. Whereas Morlet and Symlet transform are both symmetric in shape and has no scaling function.

Implementation Methodology

The method is applied on medical image (MRI of brain), by adding speckle noise as Speckle noise is most acquiring noise in medical imaging. On the noisy image soft and hard thresholding followed by wavelet based thresholding techniques for wavelet transforms family i.e. Daubechies, Haar, Symlet, Morlet are applied.  Soft and hard thresholding is applied at the rows and columns of the image. Whenever a hard thresholding is applied it gets the details of that image and whenever a soft thresholding is applied on the image it brings the approximate value. The soft and hard thresholding is applied again on the approximate and detailed value where we get the horizontal, vertical and diagonal components of the image as shown in the figure 2, 3 and 4. Comparison is being made on basis of some evaluating parameters like Peak Signal to noise Ratio (PSNR), Signal to noise Ratio (SNR) and Mean Square Error (MSE), while the decomposition level is kept constant for the evaluation tabulating in table 1. Figure 5 representing graphical interpretation of performance parameters calculated for various wavelet transforms family such as haar, morlet, symlet, Daubechies in denoising a medical imaging resonance of brain.

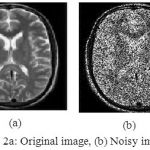Figure 2a: Original image, (b) Noisy image     Click here to View figure

 

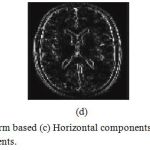Figure 3: Wavelet transform based (c) Horizontal components, (d) Vertical components, and (e) Diagonal components.   Click here to View figure

 

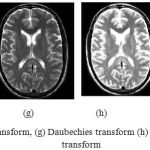Figure 4f: Morlet transform, (g) Daubechies transform (h) Symlet transform (i) Haar transform   Click here to View figure

Table1: Comparison of SNR, PSNR and MSE of various images

Type of image	Hard SNR	Soft SNR	Hard PSNR	Soft PSNR	Hard MSE	Soft MSE
Original image	13.01	13.20	56.37	56.98	0.0067	0.0094
Noisy image	9.01	8.58	34.92	35.99	0.0090	0.0135
Morlet transform	15.07	15.17	56.06	56.44	0.0067	0.0110
Haar transform	14.59	14.60	55.20	55.24	0.0086	0.0130
Daubechies Transform	16.87	16.95	56.48	56.69	0.0074	0.0116
Symlet Transform	16.89	17.01	56.58	57.02	0.0068	0.0104

 

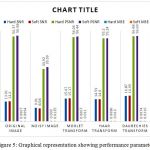Figure 5: Graphical representation showing performance parameters   Click here to View figure

Conclusion

Most of the ailments are diagnosed by clinical practitioners using medical imaging methods like MRI, CT scan, etc. One problem that medical doctor encounter while diagnosis is the low quality of medical image. For denoising medical images numerous method has been proposed of which wavelet thresholding based denoising method is more efficient and effective. In this paper we have proposed a comparison of four wavelet based image denoising techniques, which also includes soft and hard thresholding schemes. Performance is measured and analyzed using quantitative performance parameters like PSNR, SNR and MSE. Based on the statistical measures and visual quality of MRI image Symlet Transform outperformed other wavelet transforms. Further decomposition level based comparison can be performed to obtain more accurate results.

References

1. C. Gonzalez and R. E. Woods, “Digital image processing”, 2nd edition, Addison-Wesely, (2004).
2. Rafiee J, Rafiee MA, Prause N and Schoen , “ Wavelet basis functions in biomedical signal processing,” Expert System Appl 38,2011, Pages.6190–6201.
3. Katkovnik V., Egiazarian K. and Astola J., “A spatially adaptive nonparametric image deblurring”, IEEE Transactions on Image Processing, Vol. 14, No. 10 (2005) 1469- 1478.
   CrossRef
4. Sugandha Agarwal, “Analysis of linear filtering techniques on X Ray”, ICCCT 2014, (IEEE Communication Society).
5. Luo, “An efficient detail-preserving approach for removing impulse noise in images,” IEEE Signal Processing Letters, vol. 13, no. 7, pp 413–416, 2006.
   CrossRef
6. Satyadhyan Chickerur, Aswatha Kumar, “A Biologically Inspired Filter For Image Restoration”, International Journal of Recent Trends in Engineering, vol 2, no. 2, (2009)
7. Xu Y, Weaver B, Healy D M, et al. Wavelet transform domain filters: A spatially selective noise filtration technique [J]. IEEE Transactions on Image Processing, 1994, 3(6) : 217～
8. Grace Chang, Bin Yu, Martin Vetterli , “Adaptive Wavelet Thresholding for image denoising and compression,” IEEE Transaction On Image Processing, Vol.9, No.9, September 2000
   CrossRef
9. Savita Gupta, R.C. Chauhan and Lakhwinder Kaur, “Image denoising using Wavelet Thresholding,” ICVGIP 2002, Proceedings of the Third Indian Conference on Computer Vision, Graphics Image Processing, Ahmedabad, India, 2002.
10. DONOHO D L. De-Noising by Soft-Threshold .IEEE Transactions on Information Theory, 1995, 41(3):613-627.
    CrossRef
11. Bhardwaj, M. Singh, “A Novel approach of medical image enhancement based on Wavelet transform, ” International Journal of Engineering Research and Applications (IJERA) ISSN: 2248-9622,Vol. 2, Issue 3, May-Jun 2012, Pages.2356-2360.
12. Rakesh Kumar and B.S.Saini,“Improved Image Denoising Techniques Using Neighboring Wavelet Coefficients of Optimal Wavelet with Adaptive Thresholding,” International Journal of Computer Theory and Engineering, Vol.4, No.3, June 2012.
13. Anutam and Rajni “Performance Analysis Of Image Denoising With Wavelet Thresholding Methods For Different Levels Of Decomposition” The International Journal of Multimedia & Its Applications (IJMA) Vol.6, No.3, June 2014.
14. Donoho D L, John stone IM. Ideal spatial adaptation via wavelet shrinkage [J]. Biometrika, 1994, 81 (3): 425-455.
    CrossRef
15. Mallat S, Hwang W L. Singularity detection and processing with Wavelets [J]. IEEE Transactions on Information Theory, 1992, 38 (2) : 617～
    CrossRef
16. Arivazhagan, S.Deivalakshmi, K.Kannan,Performance Analysis of Image Denoising System for different levels of Wavelet decomposition,” International Journal of Imaging Science and Engineering (IJISE), Vol.1, No.3, July 2007.
17. L.Donoho and I.M.John stone. Adapting to Unknown Smoothness via Wavelet Shrinkage [J]. Journal of American StatAssoc, vol.12, pp.1200- 1224, 1995.
    CrossRef
18. Sethunadh R and Tessamma Thomas, “Spatially Adaptive image denoising using Undecimated Directionlet Transform,” International Journal of Computer Applications, Vol.84, No. 11, December 2013.
19. Kother Mohideen Dr. S. Arumuga Perumal, Dr. M.Mohamed Sathik , “ Image De-noising using Discrete Wavelet transform,” IJCSNS International Journal of Computer Science and Network Security, Vol.8 No.1, January 2008.
20. B. Kekre, S.D. Thepade, V. K. Banura and A. Khandelwal, “Introducing Global and Local Walsh Wavelet Transform for Texture Pattern Based Image Retrieval,” International Journal of Computer Science and Network Security (IJCSNS), Vol.11 No.9, September 2011, Pages65- 72.
21. Singha and K.Hemachandran, “Content Based Image Retrieval using Color and Texture,” Signal & Image Processing: An International Journal (SIPIJ) Vol.3, No.1, February 2012, Pages 39-57.
22. Singh, S. Chopra, H. Kaur and A. Kaur, “Image Compression Using Wavelet and Wavelet Packet Transformation, ” International Journal of Computer Science and Technology ( IJCST), Vol. 1, Issue 1, September 2010, Pages 97-99.
23. Kashyap and G. R. SINHA, “Image Watermarking Using 3-Level Discrete Wavelet Transform (DWT),” International Journal of Modern Education and Computer Science (IJMECS), ISSN: 2075-0161, Vol.4, No.3, April 2012, Pages 50-56.
24. M.Kothari and V.V. Dwivedi, “Transform Domain Video Watermarking: Design, Implementation and Performance Analysis,” International Conference on Communication Systems and Network Technologies (CSNT), 2012, Pages 133 – 137.
    CrossRef