S. Kamatchi¹ and M. Sundararajan²

¹Sathyabama University, Jeppiar Nagar, Shollinganallur, Chennai, India.

²Bharath University, Agaram Road, Selaiyur Chennai, India.

Corresponding Author E-mail: Kamatchime@gmail.com

DOI : https://dx.doi.org/10.13005/bpj/1086

Abstract

This paper presents an efficient multiresolution, signal analysis wavelet technique to diagnose sinusitis. We describe the properties, construction and Applications of Fractional B-Spline Wavelet Transform (FrSWT) with a strong mathematical background from the B-spline family.Diagnosis of sinusitis is a quite critical issue at the clinical level as the disease shares its symptoms with several other diseases also. An early screening algorithm is required to validate the diagnosis. We compared FrSWT output for spatially varying inhomogeneous turbid medium with previously obtained Empirical Wavelet Transform output, thereby differentiating healthy and sinusitis patient in an effective manner. FrSWT algorithm validates the output to diagnose sinusitis using wavelet technique.

Keywords

Multiresolution; Wavelet; Sinusitis; Fractional B-spline Wavelet Transform (FrSWT); B-Spline; Empirical Wavelet Transform (EWT)

Download this article as: 

Copy the following to cite this article: Kamatchi S, Sundararajan M. Diagnosing Sinusitis using Fractional B-Spline Wavelet With Near Infrared Spectroscopy. Biomed Pharmacol J 2017;10(1).

Copy the following to cite this URL: Kamatchi S, Sundararajan M. Diagnosing Sinusitis using Fractional B-Spline Wavelet With Near Infrared Spectroscopy. Biomed Pharmacol J 2017;10(1). Available from: http://biomedpharmajournal.org/?p=14095

Introduction

Fractional calculus utilized in 1974 by Keith [1], which involves fractional integral and derivative.  Many reserch works were in progress in fractional calculus concentrating in a fractional derivative.   This paper mainly focusses on using fractional wavelet transform to diagnose sinusitis.  Mallat [2-3] paved a way to wavelet analysis [4] with mathematical derivation and definitions briefing about each wavelet which is quite helpful in the biomedical signal analysis [5].  Fractional Wavelet Transform [6-7] gaining popularity in signal analysis as it combines the goodness of wavelet and SWT technique. Though Fractional Wavelet Transform [8-10] proved to be a powerful signal processing tool in 1990’s itself, it is only after Unser who paved a way to the family of scaling functions, it is used for signal analysis and synthesis.  It is used here to analyze the biomedical signal recorded from sinusitis patients and compared with healthy people with the help of FrSWT.

Sinusitis [11] is a common condition due to inflammation of the lining inside the nasal cavity and the sinuses. This may be due to viral or bacterial infections and may continue for two or more weeks.  Sinuses are cavities behind the cheeks and nasal bones, eye, and forehead. The American Academy of Otolaryngology [12] summarizes several symptoms of sinusitis with major and minor infections. As it affects 35% of the population annually, it requires proper diagnosis and treatment. Imaging techniques serve the purpose of diagnosing sinusitis at its extreme condition, but earlier diagnosis [13-14] done clinically utmost in several cases.  This misleads sinusitis detection, as the symptoms were shared by quite a few diseases also.  So, a compact, user-friendly, non-radiative, less expensive method is required.

Near Infrared Sensor (NIR) can be used to diagnose sinusitis in a non-radiative manner. It provides high resolution spatially and temporally which may attract the user to proceed with this new technique. This paper briefs about the properties, construction, and Applications of Fractional Spline Wavelet Transform (FrSWT) and to detect sinusitis in an efficient manner using NIR sensor.

Fractional Spline Wavelet Techniques

Insight to Fractional Spline Technique

A new wavelet technique based on scaling functions utilized to analyze signals.  Wavelet techniques play a critical role in the signal analysis. Splines and wavelets are strongly related and expressed in analytical form. B-Splines stability makes it attractive for specialists.  It requires very less degree of support, even the origin.  The Recursive family of B-splines can be generated using factorization theory.

The Polynomial splines, at first introduced by Schoenberg [15-16] in 1946 and later extended by Thierry Blu and Michael Unser in 2000 to fractional degrees α > -1/2. Polynomial spline is a piecewise function of order, n. Isolated discontinuities occur at the knots, joining points between polynomial segments. Fractional splines behave exactly like integer B-spline but offer extensive support for various applications. A polynomial of degree, n expressed as arithmetic relation of the scaling function.

Moreover, orthogonal fractional spline wavelet [17] can be implemented as fractional differentiator for fractal signals and fractional Brownian motions. Two commonly used approaches in splines were Orthogonal, semi-orthogonal compactly supported spline wavelets and symmetric compactly supported wavelets developed by Cohen, Daubechies, and Feauveau not confining to spline space.

Properties of Fractional B-Spline

Some of the attractive properties of fractional B-splines commonly shared with classical B- spline, discussed in brief.  Fractional splines have a fractional order of approximations. For non-integer α, it could not make an equivalency between the order of approximation, L and the polynomial degree, n. For integer, α > -1/2 fractional B-splines provide multi-resolution analyses even though it cannot produce optimal wavelet bases for integers (-1/2< α <0).  It also satisfies the two-scale relation and contributes optimal Riesz bases. Fractional splines used in variational interpolation problems even. It interpolates between polynomial degrees. It interpolates polynomial splines similar to factorial interpolation using gamma function (generalization property).  Regularity property implies that they are α- Hӧlder Continuous. They decay in such a way that even their causal polynomials becomes compactly supported. They are deficit in positivity and compact support alone.

Experimental Works and Methods

This section enables us to learn about the basic idea and construction of B-spline and fractional B-spline technique. The proposed methodology along with the database and the method of examination were presented in detail.

Fractional Differential Operators

The Fourier transform of the discrete fractional differential operator, ∆ ^γ  of order ^{γ ε R+} is given by the equation [18-20];

Here ‘+’ refers to the causal function.  The inverse FT is

Computed by applying generalized binomial expansion, the fractional forward finite difference operator (convolution operator) is

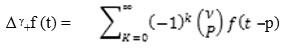
Fractional B-Spline

Fractional causal B-splines constructed by considering the analogy of classical B-splines by finite fractional differences of the symmetric and piece wise power functions which is a continuation of polynomial splines for all non-integers, α > -1.  Fractional B-splines expressed as,

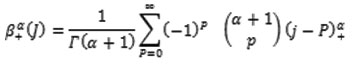
The generalized fractional binomial coefficients:

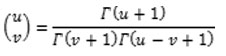
Where Ѓ(u), Euler’s Gamma function defined as Ѓ(u) =  x^u-1e^-xdx

Symmetric fractional B-splines were used to know the inner products of fractional B-spline with degree, α >-1 Β_*^α = β₊^(α-1)/2 * β_–^(α-1)/2

Overview of Orthogonal Spline Wavelet Design and Estimation

Orthogonal Spline wavelet transform first developed by Battle and Lemarie in 1987, later impelemented by Mallat and  Daubechies illustrated compactly supported transform for signal analysis. Wavelet Transform decomposes the signal into two basis functions.  Scaling function, ϕ (t) and Wavelet function, ψ(t) are the basis function estimated using scaling filter coefficient, g(n) and wavelet filter coefficient, h(n) respectively.  The Wavelet Coefficient represents the details of the signal acts a high-pass filter and the scaling function representing the approximate signal like low-pass filter.  Decomposition and reconstruction of these signals were done using tree algorithm.

Designing Orthogonal Wavelet Transform requires scaling function estimate, ϕ (t) and the filter coefficients, h (n) and g (n).  Design procedure can be initiated by selecting any one of the parameters. Battle and Lamerie started designing by selecting the scaling function, but the output suffers from non-compactly supported wavelet functions.  Later, Daubechies designed the wavelet transform considering the filter coefficients, thereby constructed a compactly supported orthonormal bases wavelet.  Pyramid algorithm used to implement the wavelet transform using low pass and high pass filter.

Orthogonal Spline wavelet can be implemented [21] by successive decomposition of approximate signals and detail signal for a maximum number of wavelet scales.  Implementation done by deciding the impulse response coefficient of the filter coefficients and then estimate the approximate and detail signal by downsampling and upsampling respectively leading to efficient and fast computation than Fourier transform.  This method is quite efficient for analysis and synthesis of signals, especially for biomedical signals.

Characteristics of Paranasal Sinus and Optical Properties of A Turbid Medium

Paranasal sinuses (PNS) comprises of narrow, air-filled cavities surrounding the nasal cavity.  Four paired sinuses [22] were Frontal, Maxillary, Sphenoidal and Ethmoidal which lies between the eyebrows, inferior to eye in maxillary bone, at the center of the head near the optic nerve and between eyes and nose separating the brain from nasal cavity respectively.  Nasal cavities and sinus cavities were connected by Ostia to allow air and mucus flow freely.  When infection occurs, this passage is blocked causing disturbance to the flow which creates pain in the sinus cavities.  The Nasal blockage may be due to viral or bacterial infection which suspends tiny particles of microorganisms, dust or allergens.  The nasal fluid becomes turbid due to such particles, which prevents easy flow of air and mucus through the cavity.

Near Infrared (NIR) [23] light [750-1100) nm offers high transparency to light and greater depth of penetration in the biological tissues (translucent).  Biophotonics field offers an ultimate diagnostic feature in exploiting the tissue-light relationship based on reflection, absorption, scattering, fluorescence and diffuse reflectance.  As per Beer Lambert’s Law, light undergoes attenuation in relation to the property of the material.  However, turbid medium (within most of the biological tissues) highly scatters the NIR light due to various molecular interactions and so non-linear attenuation occurs.  Multiple scattering occurs as different molecular interactions, exhibit various wavelengths leading to multiple frequency signal output.  Scattering [24] occurs when there is a difference in the refractive index with the material or within the material.  Air-filled cavities exhibit less absorption and reduced scattering coefficient compared to nasal cartilage [25].

Optical properties describing the photon transmission inside the turbid medium were absorption coefficient, μ_a, scattering coefficient, μ_s, refractive index, n_ref and scattering anisotropy factor, g [26].  Variation in the refractive index [27] produces scattering which can be best illustrated using Maxwell’s equation.  Photon transmission inside the tissues can be analyzed analytically using Radiative transfer equations (RTE) or modeled using Monte Carlo simulations (very expensive).  When absorption is less than the scattering coefficient, then it allows photons to propagate for large tissue volume before getting absorbed.  Turbid media scatters more than being absorbed validating the diffusion approximation to Boltzmann’s transport equation in determining μ_a and μ_s.  Photon transport [28] in highly scattering medium reduces the independent variables involved in RTE leading to diffusion theory under the assumption of directional broadening.  Transport equation reduces further when radiance becomes a function of isotropic fluence rate and directional flux in the case of a highly scattering medium.

As turbid media undergoes multiple scattering leading to total internal reflection (TIR), it necessitates the measurement of a complex refractive index.  The diffusion approximations for determining varying refractive index were discussed in many papers [29-31] with controversies to deal with spatially varying refractive index.  To resolve discrepancies of Fresnel’s equation for TIR, few researchers [32] work with angle dependent penetration.  Detecting in-homogeneities in the turbid medium is quite important in biomedical optics. In optics [33], photon path bends in an inhomogeneous medium calculated by Bouguer’s equation.  The photon transport equation [34] re-derived for isotropic, variable refractive index with spatial resolution in a highly turbid medium.  Two equations derived with trajectory photon path and the standard format in case of constant refractive index, scatter less and lossless medium.

Database

Patients registered to undertake the examination, included in the study after getting their consent.  Clinical findings, objective findings, and history of symptoms identified and given preference to undertake the study and went on immediate examination through radiographic technique.  Fifty subjects included, along with the patients with history and objective findings.  Data recorded in Sathyabama University under the supervision of a medical practitioner.  Signals recorded for 20 sec using sigview software using the prototype hardware [35] developed earlier.  Chronic patients and normal people were also included for the study.  Signals recorded using NIR sensor is further processed using signal processing tool to evaluate the findings from the hardware with the radiographic results.  Recording of signal sample is available in the link provided https://www.youtube.com/watch?v=pIItyK1Hp0A&feature=youtu.be.

Measurement Method

Signals recorded from the patients using hardware, radio graphic images and results along with the signal processing output processed and compared to diagnose sinusitis. Fractional B-Spline wavelet generates a smooth output for a piece wise continuous signal.  Wavelet analysis proves to diagnose sinusitis accurately.

Simulation

Results nd Discussion

Patient’s signals recorded under the supervision of a medical practitioner in Sathyabama dental hospital.  Patients with the history of sinusitis, Clinical symptoms, and objective findings included in the study along with the patient enrolled for the study.  Healthy subjects also included for validating the study after getting the consent of the individual subjects.  NIR sensor used to record signal from individuals for 20sec with the help of Sigview software and stored separately for normal and diseased.

Signals recorded were processed using Fractional Spline Wavelet Transform in Matlab to analyze signals in piecewise fashion, and it is represented in time-fractional–domain representation simultaneously.

Previously, we tried with Least Square Support Vector Machine (LS_SVM) classification algorithm [35] and compared normal, and sinusitis signal with each and every received FFT value and deviation from the normal curve confirms the condition in the chest.  Later, the same signals were analyzed [36] using Empirical Wavelet Transform (EWT) and Multiple Decomposition Empirical Wavelet Transform (MUSIC-EWT).  These techniques accurately generate instantaneous frequencies from a non-stationary and non-linear signal even with poor SNR.  Thus it proves to be optimum in case of real signals where noise interference and spurious signals generate within the human body.  However, it lags strong theoretical proof which fails to explain the non-linear behavior of the algorithm.

Then, we move on to Fractional Spline Wavelet Transform (FrSWT) to analyze the signal in a piecewise manner to smoothen the output at various levels.  We can get more detailed information as the signals were considered fractional.  It has strong theoretical derivation which best illustrates the algorithm.

Figure 1a: Original Signal (b) Sub-band signal (c)Fractional Spline Wavelet Transform output (d) Re-synthesized signal (e) Scaling and Wavelet Functions of Fractional Spline Wavelet Transform output of a chronic sinusitis Patient Click here to View figure

 

Using Fractional Spline Wavelet Transform, the recorded signals processed.  The signal decomposes at four levels with an alpha = 2.4 and τ = 0.3 of ortho type.  Signals separated into a low pass and high pass using FIR filter.  The high pass filter represents the impulse filter coefficient of the wavelet function which provides approximate signal, and the low pass filter represents the scaling filter coefficient of the scaling function representing the more detailed information of the signal.  Further, it is resynthesized, scaled and wavelet transform output obtained.

The output produces multiple frequencies due to multiple scattering and TIR with varying refractive indices as the medium is highly turbid for acute and chronic sinusitis.  Thus, the patient with sinusitis generates multi-frequency output as illustrated in fig.1 for a chronic patient.   Fig. 1(a) represents the original signal of a sinusitis patient.  Fig. 1(b) represents the sub-band obtained for the signal taken for study.  Fig.1(c) represents the Fractional Wavelet transformed output decomposed into four levels with an alpha and tau predefined.  These values can be varied, but this value gives optimum result.  Similarly, it is analyzed for several patients with acute or chronic condition in the sinus cavity to validate the result.  Low pass band representing the detailed signal and the high pass band representing the approximate signal.  When NIR light is transmitted through opacified sinus cavities using NIR sensor; the light gets reflected, absorbed, scattered and diffused.  Due to water accumulation, there is a more chance of TIR and less absorption at NIR range.  Multiple scattering offers diffused photon path well explained by transport equation discussed earlier and thereby generates multiple frequencies owing to total internal reflection of varying refractive index.  Fig.1 (d) illustrates the de-synthesized signal from the low pass band, combining the features of both detail and approximation signal in to approximate signal with more précised details by up sampling.  Fig. 1(e) represents the scaling and the wavelet function obtained for the sinusitis signal.  However, for a normal person, the output consists of one or very few frequencies with less high pass band.  Thus, the normal person’s sinus cavity (fully aerated) allows greater penetration of light with no loss of signal.  Light penetrates through the air-filled sinus cavities whereas; it undergoes reflection, absorption and scattering when passed through opacified cavities.

A comparison made with the normal and diseased signal using Fractional Spline Wavelet Transform along with the radiographic images taken consecutively while recording the signal with the consent of the patients.  This avoids further discrepancies in analyzing the data obtained at various instants.  Fig. 2 shows the comparison of normal and diseased FrSWT output with the radiographic images.

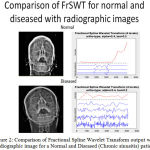Figure 2: Comparison of Fractional Spline Wavelet Transform output with radiographic image for a Normal and Diseased (Chronic sinusitis) patient   Click here to View figure

 

Likewise, the comparison made with the previous output obtained using Empirical Wavelet Transform (EWT) with the FrSWT as shown in Fig.3.  This output represents the radiographic image with Time-Frequency representation of EWT and the Time- Fourier domain representation of Fractional Spline Wavelet Transform.  In both EWT and FrSWT, sinusitis patients show multiple frequencies and the normal person shows very few variations in frequency.

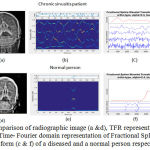Figure 3: Comparison of radiographic image (a &d), TFR representation of EWT (b &e) and Time- Fourier domain representation of Fractional Spline Wavelet Transform (c & f) of a diseased and a normal person respectively Click here to View figure

 

The Orthogonal Spline wavelet transforms analyze and synthesis signal at its best.  The output shows that the diseased signal multi-scatters with multiple approximate signals in the high pass band and less low pass band to represent the detailed signal. However in normal case, the LPF represents more details about the original signal with a resolution of 2^2j whereas it is 2^j for approximate signals. J is the no. of maximum wavelet scales.  Thus this transforms best suits for analyzing biomedical signals.

Conclusions

Near Infrared Sensor used successfully to diagnose sinusitis with the help of prototype hardware.  Fractional Spline Wavelet Transform used to analyze the signal in fractional order to improve the resolution of the output signal. Multiple frequencies generated, as the signals scatter due to various refractive index of fluid inside the sinus cavity.  Sinusitis diagnosed easily by the amount of fluid inside the cavity, generating multiple frequencies.  For aerated normal person, light penetrates through the cavity without attenuation or scattering leading to single frequency output.  Thus, an efficient algorithm has been developed to identify the turbidity of the sinus cavity and to diagnose sinusitis without undergoing radiation imaging techniques.  This paper compares the output obtained from the hardware with the radiographic image and the Empirical and Fractional Spline Wavelet Transforms in an efficient, cost-effective and non-radiative manner.  The diagnostic procedure of identifying sinusitis, simplified at an early stage.

Acknowledgment

The authors wish to thank the management of Sathyabama University for rendering their support towards the work in facilitating testing on patients and data collection in Sathyabama Dental hospital and our sincere thanks goes to the patients who volunteered for this study.

References

1. Keith B. Oldham Jerome Spanier, “The fractional calculus, Theory and applications of Differentiation and integration to arbitrary order” Academic Press Inc. London 1974.
2. Stephane Mallat, “A Theory for Multiresolution Signal Decompositon: The Wavelet representation” IEEE Transact. On Pattern Analysis and Machine Intelligence, Col.11, No.7, pp.674-693, Jul. 1989.
3. Stephane Mallat, “A Wavelet tour of Signal Processing”, Academic Press,San Diego, 1998.
4. Chui, C.K. An Introduction to Wavelets. San Diego: Academic Press, 1992.
5. Akay, M. Detection and Estimation of Biomedical signals, San Diego: Academic press, 1195.
6. K. Chui and J. Wang, “On Compactly supported spline wavelets and duality priniciple, Trans. Amer. Math. Soc. 330(992), pp. 93-916.
7. J. Lai, “On Computation of Battle- Lemarie’s wavelets, Math. Comp. 63 (1994), pp. 689-699.
8. Unser, Splines: a perfect (t for signal/ Image Processing, IEEE Signal Process. Magazine 16 (6), pp. 22-38, 1999.
   CrossRef
9. Unser, T. Blu, Fractional Splines and wavelets, SIAM Rev. 42(1), pp.43-67, 2000.
   CrossRef
10. Unser, A.Aldroubi and M. Eden, A family of polynomial spline wavelet transforms, Signal Processing, 30, 141-162, 1993.
    CrossRef
11. D. Lanza and D. D. Kennedy (1997), “Adult rhinosinusitis defined”, Otolaryngol.-Head Neck Surg., 117, S1–7.
    CrossRef
12. Fokkens W, Lund V, Mullol J (2007), “European position paper on Rhinosinusitis and Nasal polyps, Rhinology”, Vol. 45(supp.20):,1-139.
13. Hwang, A. Getz, M. Aronson et al (2010), “Acute sinusitis and rhinosinusitis in adults” (UpToDate, 2010), www.uptodate.com.
14. Jarvis D, Newson R, Lotvall J, Hastan D, et al, “P: Asthma in adults and its association with chronic rhinosinusitis: the GA2LEN survey in Europe. Allergy”, 67(1), pp. 91–98, 2012.
    CrossRef
15. J. Schoenberg, Contribution to the problem of approximation of equidistant data byanalytic functions, Quart. Appl. Math. 4 (1946), 45-99, 112-141.
    CrossRef
16. J. Schoenberg, On spline functions, In ”Inequalities”, (O. Shisha ed.) (1967), 255-291.
17. Okkyung cho and Ming Jun-Lai, “A Class of Compactly Supported Orthonormal B-Spline Wavelets”, Splines and Wavelets: Athens 2005, pp. 123-151.
18. Blu and M. Unser, “ The fractional spline wavelet transform: Definition and implementation”, in Proc.  IEEE Int. Conf. Acoust., Speech, Signal process., Istanbul, Turkey, June 2000, Vol. I, pp. 512-515.
19. Blu and M. Unser. A complete family of scaling functions: The (α,τ)- fractional splines.  In Proc. Int. Conf. Acoustics, Speech, and Signal Processing, volume VI, pages 421-424, Hong Kong SAR, People’s Republic of China, April 6-10, 2003.
20. Michael M. Unser, “ Fractional Splines Wavelet Bases and Applications, Jan 2004.
21. Metin Akay, ”wavelets in Biomedical Engineering”, Annals of Biomedical Engineering, Vol. 23, pp.531-542, 1995.
    CrossRef
22. Jing Huang, Hao Zhang, Tianqi Li, Huiying Lin, Katarina Svanberg, Sune Svanberg, “Assessment of human sinus cavity air volume using tunable diode laser spectroscopy, with application to sinusitis diagnostics”, J. Biophotonics 8, No.11-12, pp.985-992, 2015.
    CrossRef
23. F.Jobsis (1977), “Non-invasive infrared monitoring of cerebral and myocardial oxygen sufficiency and circulatory parameters”, Science Vol. 198, 1264-67.
    CrossRef
24. Brian W.Pogue, et al , “Characterization of hemoglobin, water, and NIR scattering in breast tissue: analysis of intersubject variability and menstrual cycle changes”, J. Biomed. Optics, Vol.9 (3), pp. 541-552, 2004.
    CrossRef
25. Usama Mahmood, Albert Cerussi, et al, “Near Infrared Imaging of the sinuses: Priliminaray evaluation of a new technology for diagnosing maxillary sinusitis, Jounal of biomedical optics, 15(3), 036011, June 2010.
26. Lihong V. Wang and Steven L. Jacques, “Source of error in calculation of optical diffuse reflectance from turbid media using diffusion theory”, computer Methods and Programs in Biomedicine,61, pp. 163-170, 2000.
27. Huafeng Ding, Jun Q Lu, William A Wooden, Peter J Kragel and Xin- Hua Hu, “ Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm”, Phys. Med. Bio. 51, pp. 1479-1489, 2006.
    CrossRef
28. Haskell; et al., “Boundary conditions for the diffusion equation in radiative transfer”.Journal of the Optical Society of America A. 11 (10): pp. 2727–2741, 1994.
    CrossRef
29. Khan and H. Jiang, “A new diffusion approximation to the radiative transfer equation for scattering media with spatially varying refractive indices”, J. Opt. A: Pure Appl. Opt. 55, pp.137-141, 2003.
30. M. Tualle and E. Tinet, “ Derivation of the radiative transfer equation for scattering media with a spatially varying refractive index”, Opt. Commun. 228, pp.33-38, 2003.
    CrossRef
31. L. Shendeleva, “Radiative transfer in a turbid medium with a varying refractive index: comment, “ J. Opt. Soc. Am. A 21, pp.2464-2468, 2004.
    CrossRef
32. R. Calhoun, H. Maeta, A. Combs, L. M Bali, and S. Bali, “Measurement of the refractive index of highly turbid media”, Optics letters, Vol.35 (8), 1224-1226, 2010.
    CrossRef
33. Born and E. Wolf, Principles of Optics, 4th ed. (Pergammon, 1970).
34. Malin Premaratne, Erosha Premaratne and Arthur James Lowery, “The Photon transport equation for turbid biological media with spatially varying isotropic refractive index”, Opt. epress, Vol.13(2), pp.389-399, 2005.
35. Kamatchi, Dr.M. Sundararajan, “Earlier diagnose of sinusitis in Frontal and Maxillary cavities using NIR radiations”, Journal of Computational and Theroetical Nanoscience, Unpublished.
36. Kamatchi, Dr.M. Sundararajan, “Sinusitis detection with wavelet analysis using Near Infrared Spectroscopy”, Proc. Of International conference on Engineering and Technology’16, Vol.5, pp.97-103, 2016.

(Visited 582 times, 1 visits today)