Anchal, Sumit Budhiraja, Bhawna Goyal, Ayush Dogra and Sunil Agrawal

UIET, Panjab University , Chandigarh,India.

Corresponding Author E-mail: aanchal813@gmail.com

DOI : https://dx.doi.org/10.13005/bpj/1415

Abstract

Image denoising is one of the fundamental image processing problem. Images are corrupted with additive white Gaussian noise during image acquisition and transmission over analog circuits. In medical images the prevalence of noise can be perceived as tumours or artefacts and can lead to first diagnosis. Similarly in satellite images the visibility of images is significantly degraded due to noise, hence the image denoising is of vital importance. There are many denoising mechanisms given in literature are able to work well on lower noise levels but their performance degrades with increasing noise levels. If higher amount of filtering is applied it leads to degradation or removal of edges from the image and hence significant information. In this paper, we proposed an algorithm in which we are able to address the problem of image denoising at higher noise levels while preserving the edge information. The standard bilateral filter does not provides good results at higher noise levels. Hence we proposed to combine robust bilateral filtering with anisotropic diffusion filtering as the anisotropic diffusion perform the smoothing of homogenous regions without blurring the edges. Experimental results show that the proposed method works better for higher Nosie levels in terms of PSNR values and Visual quality.

Keywords

Anisotropic diffusion; Bilateral filter; Image denoising; Magnetic resonance imaging; Robust bilateral filtering

Download this article as: 

Copy the following to cite this article: Anchal A, Budhiraja S, Goyal B, Dogra A, Agrawal S. An Efficient Image Denoising Scheme for Higher Noise Levels using Spatial Domain Filters. Biomed Pharmacol J 2018;11(2).

Copy the following to cite this URL: Anchal A, Budhiraja S, Goyal B, Dogra A, Agrawal S. An Efficient Image Denoising Scheme for Higher Noise Levels using Spatial Domain Filters. Biomed Pharmacol J 2018;11(2). Available from: http://biomedpharmajournal.org/?p=20743

Introduction

Image denoising aims to construct a plausible estimate of noisy image while maintaining a trade-off between noise degradation and feature preservation. The noise that can corrupt the signal is either multiplicative or additive and Gaussian noise is additive in nature. It is uniformly distributed over the complete image that is every pixel value of the corrupted image is the sum of original pixel value and a Gaussian noise value at that pixel. In image processing applications like satellite images, medical images, night mode vision applications, military surveillance, computer vision and computer graphics. The signal can affected by the Gaussian noise that emerges from many natural sources like thermal vibrations in conductors, black body radiations from earth and other warm objects and astronomical objects like sun. Image denoising is the backbone in image processing applications. The denoising performance of the various existing spatial domain filters like bilateral filters decreases with increase in noise levels. The main objectives of image denoising are: high peak signal to noise ratio (PSNR) and high resolution.

Several filtering methods to improve PSNR and visual quality of the image have been proposed in literature. Gaussian and box filters typically work well in applications where the amount of smoothing and denoising required is less. For example, they are quite effective in removing small dosage of noise from natural images, satellite images or medical images. However, when the noise level is large, and one is required to average more pixels to suppress the noise, these filters tends to do over smoothing of image features such as edges and corners. This over-smoothing can however be mitigated using diffusion filtering, where the amount of over smoothing can be controlled with size of the scale parameters and number of iterations. A classic example of this diffusion is anisotropic diffusion given by Perona and Malik 9.

Existing methods for the noise removal [10, 12 and 13] are mainly divided into time domain and frequency domain processing. In [14], an improved bilateral filter has been presented. In this paper, the image signal is decomposed by wavelet and is combined with bilateral filtering to construct a robust denoising framework. The work given in [14] was further extended by introducing a novel noise reduction scheme [1], in which the bilateral filter is used to estimate the image noise. Afterwards the fundamental energy of the original image is computed using kernel anisotropic diffusion. Then, the difference between the energy of original image and the Denoised image is calculated by setting up the local window. In [2], a fast algorithm for the 3D image has been proposed, in which the filter kernel is optimally expended into a sum of factorized terms by using standard bilateral filtering. This gives an effective solution in terms of eigenvalues of a square matrix. In [3], a fast and relatively accurate method for approximating the bilateral filter has been proposed with the condition that the range kernel is Gaussian. The algorithm had a simple implementation and competitively shows good results than other state-of-art methods in terms of speed and accuracy. In [5], Tomasi proposed a bilateral low pass filter for edge preservation and smoothing. The filter obtains two different weights according to the similarity of the positions and intensities of the pixels. Thus, it implements the bilateral low-pass filtering by calculating the weights of the pixels in the window.

The anisotropic diffusion filtering has been given in [6, 7, 9, and 15]. A novel filtering algorithm for removal of Rician noise from MRI images has been proposed in [6]. In this method standard deviation of the noise has been estimated by combining linear filters with minimum errors and partial differential equations to get better results.

Where as in [7], an efficient NLM algorithm for image de-noising method has been given that combines the Non-Local Means algorithm with a locally adaptive anisotropic diffusion method that chooses the appropriate pixels for NLM averaging process. In [9], different algorithms which used to realize a diffusion process have been introduced. The diffusion coefficient is selected which provides intraregional smoothing rather than interregional smoothing. In [15], an algorithm for denoising and edge preservation based on kernel anisotropic diffusion is presented.

A conventional approach to compute a plausible estimate of the original image from the corrupted image has been presented in [21]. In [22 and 23], the signal reconstruction using a maximum likelihood approach and computation of the Rician noise level has been proposed by J. Sijbers. Other techniques involve unbiased NLM [24]-[26] algorithms. In [27], the proposed method modified the filter to a matrix diffusion which refine its stability. Most of the denoising algorithms given in literature either tend to perform poorly at high noise levels or results in loss of edge information. Another approaches include, disabling of denoising at edges and counters. To address these issues i.e. to design a denoising algorithm which can work at higher noise levels while preserving edge information, we combine bilateral filtering with anisotropic diffusion filtering.

The paper is arranged as follows. Bilateral filtering and robust bilateral filtering for denoising of image are given in Section II. Section III presents the anisotropic diffusion filtering. Proposed methodology is given in Section IV. Results and discussions are shown in Section V .Conclusions and future scope are given in Section VI.

Bilateral Filter

Bilateral filter is widely used filter for image denoising. It is a nonlinear filter which is also referred as edge persevering filters. It basically involves the computation of weighted average of intensity values from the nearby location and substitutes each pixel intensity of image with this weighted average. The weights can be calculated from the Gaussian distribution.

The idea of bilateral filtering is to do the filtering in the range of image as well as domain of the image whereas the traditional filters to do the filtering in the domain of the image. In a two dimensional image, two pixels can be close to each other in terms of their locality which refers to as space filtering or they can be similar that is they can have nearby values and refers to as range filtering. The bilateral filter is given as:

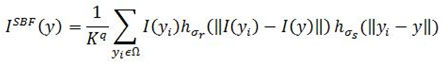
K^α Is the normalization factor which ensures that the image energy remains preserved by the filter and it is given by:

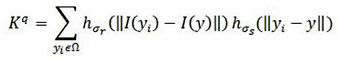
In the above equations, I^SBF  is Denoised image, I is actual grayscale image, Y is the coordinates of the pixel which needs to be filter, Ω is the window which is centred about pixel,Y h_σr is the Gaussian range kernel used for smoothing in intensities of the pixels, h_σs is the space kernel used for smoothing difference in coordinates of the pixels.

To know more about bilateral filter, consider a pixel of an image located at (p,q) that is to be filtered with the help of its nearby pixels. Let a nearby pixel located as (r,s). Then, the weight assigned to pixel (r,s) used to denoise the pixel at (p,q) is given by:

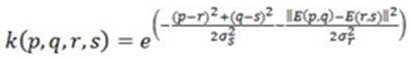
In the given equation,

and

are the smoothing parameters and E (p,q) is the intensity of pixel at location (p, q) similarly E(r,s) is the pixel intensity of the pixel at location (r,s) Once the weights have been calculated, after that there is need to be normalize them by using following equation:

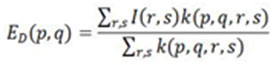
Where E_D is the intensity of the Denoised pixel at location (p,q). The bilateral filtering can also be defined in integral form as given below. A low pass filter is apply to an image F(i) to produce the output image as follows:

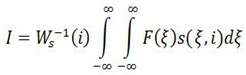
Where s(ξ,i) measures the geometric closeness between the neighbourhood centre i and a neighbouring point ξ. Similarly the range filtering is given as:

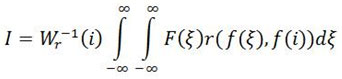
Where r(f(ξ), f(i)) measures the photometric similarity between the neighbourhood centre  and a nearby point ξ. The more appropriate and efficient solution is to combine the filtering in range and space domain, which uses both geometric locality and photometric similarity of pixels. The combined filtering can be given by:

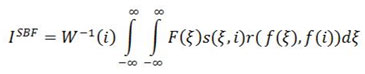
Where the normalization factor can be given by:

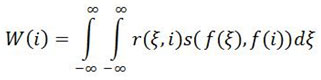
Thus, the pixel value present at i is substituted with an average of similar and nearby pixel values. Bilateral filter is easy to understand, adapt and set up yet it has some limitations like it does not work well for higher noise levels (σ>20). To address this problem modified bilateral filter known as robust bilateral filter was proposed. However it was also not able to preserve the edges for higher noise levels. For the higher noise levels and to preserve the edges and fine details of image we have combine the robust bilateral filter with anisotropic diffusion filter.

Robust bilateral filter

The standard bilateral filter can be modified by using box filter, so that it works better at higher noise values. This modified filter was design to work efficiently for higher noise value (σ= 30, 40, 50). But it does not able to perform below a threshold value (σ<30). To get the best results at all noise levels, we proposed to combine the robust bilateral filter with anisotropic diffusion filter.

Consider grayscale input MRI image

I_o(i) which is made noisy with Gaussian noise N is given by:

The Denoised image obtained by robust bilateral is given by:

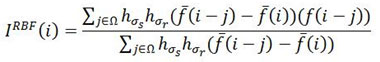
Where,

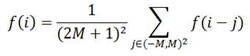
Where,

and

h_σr are h_σs the Gaussian kernels named as range kernel and spatial kernel respectively. Also the domain Ω is restricted to Ω = [-W, W] x [-W, W]. Where W=3^σs.

The main objective in RBF is to set the range (σ_r) and space (σ_s) parameters in order to get the best PSNR values. The range parameters are proportional to edge strength. As it increases, the filter approaches to the Gaussian convolution more closely because the range Gaussian expends, which states that it comes to saturation over the intensity interval of the image. In the same way the space parameters are proportional to image size i.e. 2% of the image size. As it increases, the larger features of image get smoothened.

The smoothing and blurring done by the box filter, whose amount  depends  on the factor M. The simulation results depict that M = 1 is optimal value for experiment. It is a conceivable method which is able to reduce the noise without much blurring the important details of image. The filters parameters and are selected in order to get the best PSNR. The robust bilateral filter performs better at higher noise level (σ=30 to 50). At lower noise values (σ<30), the box filter induce more blurring effects than denoising that degrades the overall peak signal-to-noise ratio. However, at higher noise levels RBF removes the edges and fine details of the image hence there is loss of important parts of the image. To solve this problem RBF is cascaded with the anisotropic diffusion filter.

Anisotropic diffusion filtering

In robust bilateral filtering, local image variation computes at every pixel value of image, and pixel values are normalized from the neighbouring pixels whose physical characteristics depend on local variation. This filtering mechanism fails at edges, which gets blurred by low pass filtering, hence there where, is a loss of significant parts of image. Many techniques have been proposed to diminish this effect. Anisotropic diffusion gives the comparatively best results. In Diffusion methods partial differential equations are iteratively solved by averaging over extended regions. This Iteration may raise issues of stability and efficiency.

Anisotropic diffusion also known as Perona and Malik diffusion. It is a method of image denoising in which filtering is perform without removing the significant parts of image like edges, lines or any other important details. There is important parameter in this diffusion process termed as scale space in which the diffusion process creates the parametric family of images with increasing amount of blurring in successive manner. Each of the blurred image is obtained by convolving the original image with the isotropic filter. The width of this filter increases with the parameter.

In the proposed method, the fundamental energy of the image is computed by robust bilateral filter. But the accuracy of fundamental energy of the noisy image is of major concern because the energy of the noised image manifests the basic information of the original image. Therefor the anisotropic filter is applied to pre-process the noisy image and compute the fundamental energy. The anisotropic filter is define as:

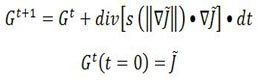
Where ∇ is gradient operator, ||b|| gives Magnitude, s(||∇j||) is the diffusivity function or also called as “edge-stopping” function. Div is the divergence operator. G^t Represents the fundamental energy of the noised image at t iteration.is the time step of each iteration ∇t. The diffusion function can be given by the following equation.

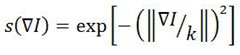
As the number of iterations increases, image will become smoother. As a result there is loss of fine details of the image. Further, to obtain the modified P-M equation, regularization should be done. But blurring cannot be completely avoided even after regularization. To mitigate this effect, the regularization parameter should be chosen wisely by taking care of noise value. The modified PM equation given as:

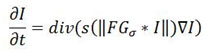
As the number of iterations increases, image will become smoother. As a result there is loss of fine details of the image. Further, to obtain the modified P-M equation, regularization should be done. But blurring cannot be completely avoided even after regularization. To mitigate this effect, the regularization parameter should be chosen wisely by taking care of noise value. The modified PM equation given as:

Where,

Anisotropic diffusion filtering is a very efficient method for image denoising if parameters are selected properly. Along with the image denoising, anisotropic diffusion can be used in edge detection algorithms.

Objective metric

Objective metric analysis is a key step in the evaluation of image processing algorithms and is vital for validation of any kind of image processing algorithm [28-46].The Peak Signal to Noise Ratio (PSNR) and Mean Square Error (MSE) are the two error metrics used to demonstrate the image quality. The PSNR is the measure of the peak error whereas MSE gives the squared error between the noised and the clean image.

The PSNR is the peak signal to noise ratio between the uncorrupted image and noisy image. It quantifies in decibels (db). This ratio is generally used as a quality estimation between the original and a noised image. It is known that higher the PSNR, better the quality of the Denoised image and better the denoising algorithm.

To compute PSNR, first we will calculate MSE by given equation.

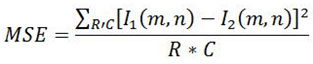
Where R is the number of rows and C is number of columns in the input image. The mean squared error (MSE) compare the true pixel values of original image with corrupted image and gives the average of the squares of the errors between original image and noised image. The error is the amount by which the pixel values of the clean image differs from the pixel values of the noised image. Once the MSE has been computed, after that PSNR will be calculated which is given by:

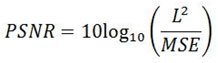
Where L is maximum number of variation in the input image. For example, L is 255 for an input image of 8-bit unsigned data type.

Proposed Methodology

In this section, the steps of the proposed algorithm are listed in table 1. We propose a combinational approach of bilateral filter and diffusion filtering towards image denoising, to attain a reasonable amount of denoising even at higher noise levels, while preserving the fine features, details and edges as shown in figure 1.

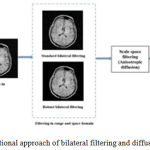Figure 1: Combinational approach of bilateral filtering and diffusion filter   Click here to View figure

 

Table 1: Steps for the proposed methodology

1	The input image is estimated with varied values of Gaussian standard deviation i.e. 10, 20, 30, 40 and 50.
2	The standard data sets of MRI, PAN and House are taken in order to analyse the versatility of the proposed algorithm. The standard deviation values of noise i.e. 10 and 20 are taken as lower noise values, 30 is taken as a moderate amount of noise and 40 and 50 are taken high values of noise. The input images are 256*256, 8-bit grey scale images.
3	Initially the noisy images are filtered in the range and the space domain using standard bilateral filter (SBF) and robust bilateral filtering (RBF). The value of range kernel is taken as 20 and space kernel as 4.
4	The output of the SBF and RBF is found to have residual noise at values of Gaussian standard deviation. The output of both SBF and RBF are further smoothened using anisotropic diffusion filtering individually. The value of gradient modulus threshold is taken as 15, nabla as 0.15 and number of iterations as 2.
5	The output image is objectively evaluated by calculating the Peak-signal-to noise ratio

 

Results and discussion

We implemented the proposed RBFAD algorithm using MatlabR2014b on Intel core i5 2.20 GHz, 64-bitoperating system with 4 GB memory. The grayscale MRI image used for the experiment is shown in figure 2(a). The image is resized to 256*256 (8 bit) in the Matlab. Input MRI image is made noisy with the additive white Gaussian noise at standard deviation σ=10, 20, 30, 40, 50 as shown in figure 2(b to c). The Gaussian noise at σ= 10 and 20 is consider as low noise levels. Gaussian noise at σ=30 is consider as moderate noise level and noise at σ=40 and 50 is consider as high noise levels. We have compared the proposed algorithm with the SBF, SBFAD and RBF. The parameter settings selected for the proposed method is given in algorithm.

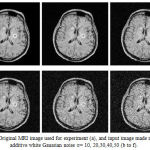Figure 2: Original MRI image used for experiment (a), and input image made noisy with additive white Gaussian noise σ= 10, 20,30,40,50 (b to f).   Click here to View figure

 

The output of the proposed algorithm on MRI image for different noise levels σ= 10 to 50 is shown in figure 3(d). We also present the output obtained by SBF, SBFAD and RBF and compared these outputs with RBFAD. It can be clearly seen from the filtered images (fig 3) that standard bilateral filter works well on low noise levels buit is not able to preserve edges and fine details of the image. To preserve edges standard bilateral filter is cascaded with anisotropic diffusion. This mechanism can preserve the edges but only for low noise levels not for the moderate and high noise levels. For high noise levels robust bilateral filter is used but it also does not preserve edges for the high noise levels. To solve the problem of denoising and edge preservation at high noise levels robust bilateral filter is cascade with anisotropic diffusion filter. It can be seen in figure 3(d) that RBFAD provides the best results in terms of visual quality.

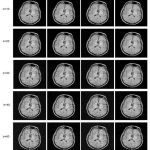Figure 3: Denoised images obtained by SBF (a), RBF (b), SBFAD (c), RBFAD (d)   Click here to View figure

 

Further, the PSNR values that have been computed for different methods is shown in table 2. From the PSNR values we can depict that SBF and SBFAD algorithms produce the higher PSNR only for low values of σ. For, σ= 40, 50 the robust bilateral filter with anisotropic diffusion provides the larger values of PSNR and it is know that higher the PSNR, the quality of image is better. Also the PSNR values varies inversely with the noise level i.e. as the noise level increase the PSNR value will be decrease. The graphs showing the relation between PSNR and noise level (σ) for the different methods is given in fig 4.

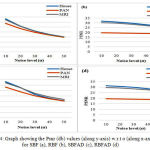Figure 4: Graph showing the Psnr (db) values (along y-axis) w.r.t σ (along x-axis) for SBF (a), RBF (b), SBFAD (c), RBFAD (d)   Click here to View figure

 

Table 2: Output PSNR in decibels for the SBF, RBF, SBFAD, RBFAD at σ= 10 to 50.

House	SBF RBF SBFAD RBFAD	33.23 31.75 33.17 31.34	26.11 30.98 27.65 30.74	20.95 29.69 21.40 29.77	17.60 28.19 17.82 28.65	15.14 26.37 15.57 27.08
PAN	SBF RBF SBFAD RBFAD	28.62 19.54 28.13 19.47	23.44 19.37 23.85 19.35	19.60 19.13 20.08 19.15	16.91 18.84 17.39 18.79	14.74 18.40 15.45 18.50
MRI	SBF RBF SBFAD RBFAD	32.18 30.20 32.08 29.60	25.78 29.65 27.58 29.20	20.79 28.54 22.45 28.49	17.44 27.13 19.05 27.57	15.13 25.63 16.79 26.36

 

Conclusion

We presented a novel and efficient Image Denoising Algorithm using spatial domain filters. The proposed algorithm is compared with SBF, SBFAD and RBF. The performance analysis of algorithms is done by calculating image metrics such PSNR (Peak Signal to Noise Ratio) and MSE. Through the experiments perform on input MRI image we find that RBFAD provides the best results for higher noise values (σ=30 to 50) in terms of visual quality and PSNR. Whereas standard bilateral filter is suitable for low noise levels.

The performance of the proposed algorithm can be improved this method by changing the parameters of filter or by using the some other filter in place of robust bilateral filter. Also this can be modified by taking some other kind of noise in place of additive white Gaussian noise. These modifications of the proposed method will inspire the future research.

References

1. Chen yong, Zhou wenzhang. A fast de-noising algorithm based on local weighting. IEEE conference. 2017.
2. Giuseppe Papari, Nsasiru Idowu and Trond Varslot. Fast bilateral filtering for denoising large 3D image. Ieee transactions on image processing. 2017;26(1)
   CrossRef
3. Kunal N. Chaudhury and Swapnil D. Dabhade. Fast and Provably Accurate Bilateral Filtering. Ieee transactions on image processing. 2016;25(6).
4. Priyanka D. Patil, Dr. Anil D. Kumbhar. Bilateral filter for image de-noising. IEEE conference. 2015.
5. Tomasi and R. Manduchi. Bilateral filtering for gray and color images. in Proceedings International conference on computer vision. 1998;839-846.
6. Karl Krissian and Santiago Aja-Fernández. Noise-Driven Anisotropic Diffusion Filtering of MRI. Ieee transactions on image processing. 2009;18(10).
7. Weifeng Sun, Min Han. Adaptive search based non-local means image de-noising. IEEE conference. 2009.
8. Buades B. Coll and J.M. Morel. A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation (SIAM Interdisciplanary Journal. 2005;4(2):490-530.
   CrossRef
9. Perona and J. Malik. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern. Anal. Mach. Intell. 1990;12(5);629-639.
10. Knaus and M. Zwicker. Progressive Image Denoising. IEEE Transactions on Image Processing. 2014;23(7):31143125.
    CrossRef
11. Pierazzo M. Lebrun, M. E. Rais, J. M. Morel and G. Facciolo. Non-local dual denoising. Proc. IEEE International Conference on Image Processin. 2014.
12. Liu C, Freeman W. T, Szeliski R and S. Kang. Noise estimation from a single image. Proc. IEEE Computer Vision and Pattern Recognition. 2006;1:901-908.
13. M Aleksic, M. Smirnov and S. Goma. Novel bilateral ûlter approach: Image noise reduction with sharpening. Proc.Digital Photography II Conference. 2006;6069 SPI.
    CrossRef
14. Ming Zhang and Bahadir K. Gunturk. Multiresolution Bilateral Filtering for Image Denoising. IEEE Transactions on Image. 2008;17(12):2324-2333.
    CrossRef
15. Jinhua Yu, Yuanyuan Wang and Yuzhong Shen. Noise reduction and edge detection via kernel anisotropic diffusion. Journal Pattern Recognition. 2008;29(10);1496-1503.
    CrossRef
16. A Buades, B. Coll and J Morel. A non-local algorithm for image denoising. IEEE International Conference on Computer Vision and Pattern Recognition. San Diego. 2005;60-65.
17. Laparra V, Gutierrez J, Camps Valls G, Malo J. Image denoising with kernels based on natural image relations. Mach. Learn. Res. 2010;11:873–903.
18. Morillas S, Gregori V and Sapena A. Fuzzy bilateral ûltering for color images. Lecture Notes in Computer Science. 2006;138–145.
    CrossRef
19. Henkelman R. Measurement of signal intensities in the presence of noise in MRI images. Med. Phy. 1985;12(2):232–233
    CrossRef
20. Sijbers J, D. Poot A. J, den Dekker and W. Pintjens. Automatic estimation of the noise variance from the histogram of a magnetic resonance image. Phys. Med. Biol. 2007;52:1335–1348.
    CrossRef
21. Mc Gibney G and M. Smith. Unbiased signal-to-noise ratio measure for magnetic resonance images. Med. Phys. 1993;20(4):1077–1078.
    CrossRef
22. Sijbers A. J. den Dekker P. Scheunders and D. Van Dyck. Maximum-likelihood estimation of Rician distribution parameters. IEEE Trans. Medical Imagin. 1998;17(3):357–36
    CrossRef
23. Sijbers J and A. J. den Dekker. Maximum likelihood estimation of signal amplitude and noise variance form MRdata. Magnetic Resource Imag. 2004;5:586–594.
24. Manjón J.V, J. Carbonell-Caballero, J. J. Lull, G. García-Martí, L. Martí-Bonmatí and M. Robles. MRI denoising using non-local means. Med. Image Anal. 2008;12:514–523.
    CrossRef
25. Wiest-Daesslé N, Prima S, P. Coupé, S. Morrissey and C. Barillot. Rician noise removal by non-local means ûltering for low signal-to-noise ratio MRI: Applications to DT-MRI. in Medical Image Computing and Computer-Assisted Intervention, ser. Lecture Notes in Computer Science. New York: Springer-Verlag, 2008;5242;171–179.
26. S. Aja-Fernández and K. Krissian. An unbiased non-local means scheme for DWI ûltering. in Proc. Workshop on Computational Diffusion MRI. MICCAI, 2008;277–28.
27. Krissian C, Westin Kikinis and K Vosburgh. Oriented speckle reducing anisotropic diffusion. IEEE Trans. Image Processing 2007;16(5):1412–142.
    CrossRef
28. Dogra Ayush, Sunil Agrawal, Bhawna Goyal, Niranjan Khandelwal, and Chirag Kamal Ahuja. Color and grey scale fusion of osseous and vascular information. Journal of Computational 2016;17:103-114.
29. Ayush Dogra, Sunil Agrawal, Niranjan Khandelwal, and Chiraj Ahuja. Osseous and vascular information fusion using various spatial domain filters. Research Journal of Pharmacy and Technology, 2016;9(7):937-941.
    CrossRef
30. Dogra A and Sunil Agrawal. 3-Stage enhancement of medical images using ripplet transform, high pass filters and histogram equalization techniques. International Journal of Pharmacy and Technology. 2015;7:9748-976.
31. Sunil Agrawal. Bone vessel image fusion via generalized reisz wavelet transform using averaging fusion rule. Journal of Computational 2017;21:371-378.
32. Bhawna Goyal and Sunil Agrawal. From Multi-scale Decomposition to Non-multi-scale Decomposition Methods: A Comprehensive Survey of Image Fusion Techniques and its Applications. IEEE Access. 2017.
33. Yadav Jyotica, Ayush Dogra, Bhawna Goyal and Sunil Agrawal. A Review on Image Fusion Methodologies and Applications. Research Journal of Pharmacy and Technology. 2017;10(4): 1239-1251.
    CrossRef
34. Sunil Agrawal and Bhawna Goyal. Efficient representation of texture details in medical images by fusion of Ripplet and DDCT transformed images. Tropical Journal of Pharmaceutical 2016: 15(9);1983-1993.
35. Sunil Agrawal. Efficient Image Representation Based on Ripplet Transform and Pure-Let. J. Pharm. Sci. Rev. Res. 2015: 34(2,16): 93-97.
    CrossRef
36. Goyal, Bhawna, Ayush Dogra, Sunil Agrawal, and B. S. Sohi. “Dual Way Residue Noise Thresholding along with feature preservation.” Pattern Recognition Letters 2017.
    CrossRef
37. Goyal, Bhawna, Sunil Agrawal,  B. S. Sohi, and Ayush Dogra. “Noise Reduction in MR brain image via various transform domain schemes.” Research Journal of Pharmacy and Technology.2016;9(7): 919-924.
    CrossRef
38. Dogra, Ayush, and Parvinder Bhalla. “CT and MRI Brain Images Matching Using Ridgeness Correlation.” Biomedical & Pharmacology 2014;7(2): 691-696.
    CrossRef
39. Parvinder Bhalla. “Image Sharpening By Gaussian And Butterworth High Pass Filter.” Biomedical and Pharmacology Journal. 2014;7(2): 707-713.
    CrossRef
40. Manjeet Singh Patterh. “CT and MRI brain images registration for clinical applications.” J Cancer Sci Ther. 2014;6: 018-026.
41. Ayushi Arora et al., Development, characterization & processing of quantum dots for imaging in UV-visible range. International Journal of Pharmacy & Technology. 2016;8(2):12811-12825.
42. Dogra, A., Goyal, B. and Agrawal, S., “Current and Future Orientation of Anatomical and Functional Imaging Modality Fusion. Biomedical and Pharmacology Journal. 2017;10(4); 1661-1663.
    CrossRef
43. Goyal B, Agrawal S. Osseous and digital subtraction angiography image fusion via various enhancement schemes and Laplacian pyramid transformations. Future Generation Computer. 2018.
    CrossRef
44. Goyal B, Dogra A, Agrawal S, Sohi BS. Two-dimensional gray scale image denoising via morphological operations in NSST domain & bitonic filtering. Future Generation Computer Systems. 2018.
45. Dogra A, Performance comparison of different wavelet families based on bone vessel fusion. Asian Journal of Pharmaceutics (AJP): Free full text articles from Asian J Pharm. 2017;10(04).
46. Dogra A, Goyal, B., Agrawal, S and Ahuja C.K. Efficient fusion of osseous and vascular details in wavelet domain. Pattern Recognition Letters. 2017;94:189-193.
    CrossRef