Namrata Singh and Pradeep Singh

Department of Computer Science and Engineering, National Institute of Technology, Raipur-492001, Chhattisgarh, India.

Corresponding Author E-mail: nsingh.phd2016.cs@nitrr.ac.in

DOI : https://dx.doi.org/10.13005/bpj/1179

Abstract

Chronic Kidney Disease (CKD) is a major public health problem with growing challenges for its early diagnosis, timely prevention and effective treatment. The present dataset on Chronic Kidney Disease consists of 24 predictive parameters. The study performs a comparative analysis of rule based classifiers inorder to generate human interpretable rules for diagnosing CKD. Various rule-based approaches for comparison that have been used in the paper are JRip, CART, Conjunctive Rule, C4.5, NNge, OneR, Ridor, PART, and Decision Table-Naive Bayes (DTNB) hybrid classifier. The study concludes that among all the conventional classifiers cited, DTNB is best rule-based classifier with highest area under ROC (0.999) along with lowest False Positive Rate (0.011).

Keywords

Chronic Kidney Disease; classification rules; data mining; predictive analysis rule-based classifiers;

Download this article as: 

Copy the following to cite this article: Singh N, Singh P. Rule Based Approach for Prediction of Chronic Kidney Disease: A Comparative Study. Biomed Pharmacol J 2017;10(2).

Copy the following to cite this URL: Singh N, Singh P. Rule Based Approach for Prediction of Chronic Kidney Disease: A Comparative Study. Biomed Pharmacol J 2017;10(2). Available from: http://biomedpharmajournal.org/?p=14665

Introduction

Chronic Kidney Disease (CKD) is a worldwide health concern rising at a very fast pace. According to the National Kidney Foundation,¹ ten percent of the total world population is affected by CKD leading to an increased mortality rate. It is estimated that in developing countries like China and India, the cases of kidney failure will increase disproportionately where the number of elderly people are increasing due to enhanced life span. Chronic Kidney Disease is also termed as end-stage renal disease.

Kidney disease can be classified into five stages.² At the first stage, kidney functions normally but it reduces mildly at every succeeding stage. During the transition from stage 3 to stage 4, renal functions are severely reduced. End-stage renal failure occurs at last stage of CKD. CKD detected at stage 5 leads to renal replacement therapy and dialysis. With early diagnosis and treatment, the progression of the kidney disease can be stopped along with substantial reduction in treatment cost. In this way an early prediction of CKD can lead to improved quality of life.

The stages of CKD and the level of kidney function are estimated by the Glomerular Filtration Rate(GFR).³ Creatinine is a waste product that comes from muscle activity. When kidneys are working well, removal of creatinine from the blood takes place. As kidney function slows down, blood levels of creatinine rise. Stage I CKD is reported with high GFR (> 90 mL/min) and end stage CKD is detected with very lowGFR (<15 mL/min).

Figure 1: The location of kidneys in human body4.   Click here to View figure

Kidneys are two bean-shaped organs residing opposite to each other on either side of the spine. The position of right kidney is a little bit lower than the left kidney to accommodate the liver. Its core actions include extraction of waste from the blood, balancing body fluids, urine formation, blood pressure regulation, red blood cell regulation, and acid regulation.⁵ Figure 1 shows the location of kidneys in human body. This figure is adapted and modified from the reference.

The kidneys are multi-functional powerhouses of activity and aid in performing many important functions of the human body. When they do not work properly, harmful toxins and excess fluids are produced in the body which can cause kidney failure.⁶

Exosomes are cell-derived 40–100 nm membrane vesicles occurring in all eukaryotic fluids including blood, urine and other cell cultures. The diameter of exosomes are larger than low-density lipoproteins (LDL)and smaller than red-blood cells (RBCs). These⁷ exosomes play a critical role in various processes such as coagulation, intercellular signaling and waste management. Its physiological roles include exosomes as a source of protein and RNA biomarkers, as potential therapeutic agents. The failure of exosome-based therapy in endothelial cells can cause chronic kidney diseases and other health problems like atherosclerosis and hypertension. These exosomes can be potentially used for prognosis, in therapy and as biomarkers for identifying health disorders.

Related Work

During recent past, various classification methods as well as  their applications have been developed to predict CKD. In what follows, we will review and investigate related works on classification methodologies for kidney diagnosis done previously.

In the field of medical diagnosis of chronic kidney disease, Noia et al.⁸ present a classifier based on ensemble of ten artificial neural networks with the data collected over a period of 38 years. A software tool has been developed predicting the end-stage kidney disease (ESKD) risk of the patients as online web application as well as Android mobile application.

Gunasundari et al.⁹ propose two modified Boolean Particle Swarm Optimization (BoPSO) algorithms viz. Velocity bounded BoPSO (VbBoPSO) and Improved Velocity bounded BoPSO (IVbBoPSO) for solving the problem of feature selection. Both these algorithms have been tested on 28 benchmark datasets. The proposed system selects exclusive features from the datasets to achieve high classification accuracy.

Inorder to detect CKD, Salekin and Stankovic¹⁰ provide classification with feature selection methodology based on three classifiers namely K-nearest neighbour, random forest and neural networks. With the feature reduction methods namely, wrapper method and LASSO regularization, 12 attributes from 24 attributes have been selected to detect accuracy with high accuracy. Further, CKD detection has been done by reducing the number of attributes to 5.

Using WEKA data mining tool, Arora and Sharma¹¹ focus on CKD detection with eight classification methods namely SGD, Random Subspace, SMO, JRIP rules, Hoeffding tree, NaiveBayes, Locally weighted learning, oneR. Different performance measures of the resulting algorithms have also been presented.

Rubini and Eswaran¹² propose three classifiers viz. radial basis function networks, multilayer perceptron, and logistic regression for the prediction of CKD. Various performance metrics have also been calculated for the CKD dataset.

Gadaras and Mikhailov¹³ provide a fuzzy classification method for the extraction of fuzzy rule sets from the dataset for building of medical diagnosis framework. The proposed method is compared with the existing methods on three medical datasets namely Wisconsin breast cancer dataset, pima Indian diabetes dataset, and bupa liver dataset.

Krause et al.¹⁴ provide an overview on the role of exosomes in kidney growth and diseases like renal cancer. The review also includes recent research on the importance of exosomes as diagnostic markers and its therapeutic use to kidney diseases and cancers. The authors have also illustrated about the proteins found in human urinary exosomes existing in the regions of the kidney and also about the significant genes found in exosomes of the various species.

Jella et al.¹⁵ examined the regulation of epithelial sodium channels (ENaC) in mpkCCD cells. Glycolytic enzyme glyceraldehyde-3-phosphate dehydrogenase (GAPDH) was located within exosomes which were derived from proximal tubule LLC-PK1 cells. The study illustrates the importance of exosomes in the modulation of EnaC activity and in collection of the duct cells.

Materials and methods

The description of the dataset and the abbreviations used throughout the paper are elaborated in this section. The terms used all through the paper are shown in table1.

Table 1: Terms used throughout the paper

Abbreviation	Explanation
AUC	Area Under ROC Curve
CKD	Chronic Kidney Disease
DTNB	Decision Table-Naïve Bayes
EnaC	Epithelial Sodium Channels
ESKD	End Stage Kidney Disease
FN	False Negative
FP	False Positive
GAPDH	Glycolytic enzyme glyceraldehyde-3-phosphate dehydrogenase
GFR	Glomerular Filtration Rate
LASSO	Least Absolute Shrinkage and Selection Operator
LDL	Low Density Lipoproteins
PART	Partial Decision Trees
RNA	Ribo Nucleic Acid
ROC	Receiver Operating Characteristics
SGD	Stochastic Gradient Descent
SMO	Sequential Minimal Optimization
TN	True Negative
TP	True Positive

Dataset

The Chronic Kidney Disease (CKD) dataset used in this study is obtained from  UCI repository.¹⁶  The information about each attribute and its description is shown in Table 2. This dataset contains missing values for its various attributes. The missing values for nominal attributes have been replaced by modes, and numeric attributes by means from the training data. The classification of the dataset is with respect to the kidney disease as ckd or notckd. Weka classification algorithms available at¹⁷ were used for the purpose of comparative study among rule-based learners. The performance of each learner was tested using 10-fold cross validation. The CKD dataset was loaded in the WEKA classification module and trained several times to maximize the classification performance.

Table 2: Description of Chronic Kidney Disease Dataset

Name of attribute	Attribute Abbreviation	Description of attribute
Age	ag	Patient age as numeric attribute with minimum age of 2 years and maximum age of 90 years.
blood pressure	bp	BP with minimum 50 mmHg and maximum 180 mmHg.
specific gravity	sg	Nominal attribute with five distinct values.
Albumin	al	Nominal attribute with six distinct values.
sugar	su	Nominal attribute with six distinct values.
red blood cells	rbc	Nominal attribute with normal and abnormal blood counts.
pus cell	pc	Nominal attribute categorized as normal and abnormal cells.
pus cell clumps	pcc	Nominal attribute categorized as present and notpresent cell clumps.
Bacteria	ba	Nominal attribute divided into present and notpresent.
blood glucose random	bgr	Numeric attribute ranging from 22 mg/dl to 490 mg/dl.
blood urea	bu	Numeric attribute ranging from 1.5 mg/dl to 391 mg/dl.
serum creatinine	sc	Numeric attribute ranging from 0.4 mg/dl to 76 mg/dl.
Sodium	sod	Numeric attribute ranging from 4.5 mEq/L to 163mEq/L.
Potassium	pot	Numeric attribute ranging from 2.5 mEq/Lto 47mEq/L.
Hemoglobin	hemo	Numeric attribute ranging from 3.1 gms to 17.8 gms.
packed cell volume	pcv	Numeric attribute ranging from 9 to 54.
white blood cell count	wc	Numeric attribute with minimum 2200 cells/cumm and maximum 26400 cells/cumm.
red blood cell count	rc	Numeric attribute with minimum 2.1 millions/cmmand maximum 8 millions/cmm.
hypertension	htn	Nominal categorization as yes or no.
diabetes mellitus	dm	Nominal categorization as yes or no.
coronary artery disease	cad	Nominal categorization as yes or no.
appetite	appet	Nominal categorization as good or poor
pedal edema	pe	Nominal categorization as yes or no.
Anemia	ane	Nominal categorization as yes or no.
Class	class	Categorized as having CKD or notCKD.

Methodology

The prevalence of ckd in the dataset was about 62.5 % and that of non-ckd 37.5 %. We have chosen rule based classification method. The step-by-step workflow of the detection process is depicted in Figure 2. The CKD dataset has been preprocessed by removing the missing values. In order to perform 10-fold cross validation, the dataset has been divided into training and testing set. The classification model derived from the rule-based learners is applied on the testing dataset for determining the performance metrics. The whole process is conducted 10-times for averaging of performance parameters. Finally, set of rules are generated by the rule-based learners with minimal set of attributes for CKD prediction.

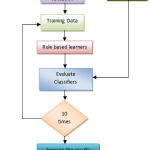Figure 2: Workflow of the CKD prediction.     Click here to View figure

Performance Evaluation Measures

This dataset has been evaluated on six different classifier performance parameters namely accuracy as defined by equation (1), true positive rate as defined in equation (2), false positive rates defined in equation (3), precision as defined in equation (4), F-measure as defined in equation (5) and area under ROC curve (AUC).

Comparative Analysis of the Rule-Based Learners

In this section, various rule base learners used for the study are elaborated and studied in context of the various performance evaluation measures such as accuracy, true positive rate, false positive rate, precision, and F-measu

Jrip

JRip¹⁸ implements a  propositional rule learner, Repeated Incremental Pruning to Produce Error Reduction (RIPPER). This algorithm is competitive with C4.5 rules in terms of error rates and more efficient on large instances and noisy datasets. It achieves an accuracy of 0.960 and ROC area 0.959.

Cart

Classification and Regression Tree algorithm was developed by Brieman etal.¹⁹ and utilizes Gini index as its splitting function. CART achieves an accuracy of 0.968 and area under curve 0.966 on CKD data set.

Conjunctive Rule

This rule implements a single conjunctive rule learner that makes predictions for both numeric and nominal class labels. The rule-based learner attains an accuracy of 0.915 and ROC area of 0.924.

C4.5

The rules generated by the C4.5 algorithm²⁰ utilize splitting criterion as gain ratio to determine the goodness of split. The accuracy achieved by C4.5 is 0.968 and ROC area 0.976.

NNge

This instance based learning method²¹ makes use of non-nested generalized exemplar to improve the performance of nearest neighbor classifier. This rule-based learner attains an accuracy of 0.988and area under curve 0.983.

Oner

This rule based learner²² classifies the instance based on a single attribute. It uses the minimum-error attribute for prediction and discretization of numeric attributes. It achieves accuracy of 0.920 and ROC area of 0.921.

Ridor

It describes an induction of Ripper-Down rules²³ to be applied for the modeling of large databases with resulting rule-sets having minimal inter-rule interactions. It achieves both an accuracy and ROC area of 0.935 each.

Part

This algorithm²⁴ creates the rules by constantly generating partial decision trees by merging two paradigms for rule making, namely, generating rules from decision trees and separate and conquer rule learning technique. It achieves an accuracy of 0.975 and area under curve 0.972.

Dtnb

DTNB²⁵, a semi-naïve Bayesian ranking method, generates the rules with combination of naïve bayes classifier and decision tables. This rule based classifier achieves an accuracy of 0.983, lowest false positive rate 0.011 and highest ROC area 0.999 as depicted in Table 3.

Rule Generation

The process of rule generation is significant for the diagnosis of kidney disease as ckd or notckd. A comparative study of the various rule-based algorithms has been proposed. The rules generated by the two rule-based algorithms namely JRip and C4.5 are as follows:

JRip generates two rules by utilizing three attributes viz. hemo, bgr and al for prediction as ckd or notckd. The rules exracted by JRip are as

R1: (hemo>= 13.1) and (bgr<= 140) and (al = 0) =>notckd

Otherwise =>ckd

The  rule R1 indicates that if hemoglobin  is greater or equal to 13.1, blood glucose random  is less than or equal to 140 and albumin is zero then notckd otherwise ckd.

Further, C4.5 rule-based algorithm generates 11 rules with the help of six attributes namely hemo, sc, sod, htn, dm and al for diagnosis of CKD. Rules generated by C4.5 are as follows:

(hemo<= 12.9) and (sc<= 1.1) and (sod <= 143) =>ckd

(hemo<= 12.9) and (sc<= 1.1) and (sod > 143) =>notckd

(hemo<= 12.9) and (sc> 1.1) =>ckd

(hemo> 12.9) and (htn = yes) =>ckd

(hemo> 12.9) and (htn = no) and (dm = yes) =>ckd

(hemo> 12.9) and (htn = no) and (dm = no) and(al = 0) =>notckd

(hemo> 12.9) and (htn = no) and (dm = no) and (al = 1) =>ckd

(hemo> 12.9) and (htn = no) and (dm = no) and (al = 2) =>ckd

(hemo> 12.9) and (htn = no) and (dm = no) and(al = 3) =>ckd

(hemo> 12.9) and (htn = no) and (dm = no) and (al = 4) =>ckd

(hemo> 12.9) and (htn = no) and (dm = no) and (al = 5) =>notckd

Table 3: Performance measures of rule-extraction methods on CKD dataset.

Rule Extraction methods	Accuracy	TP Rate	FP Rate	Precision	F-measure	ROC Area
JRip	0.960	0.960	0.048	0.960	0.960	0.959
CART	0.968	0.968	0.044	0.968	0.967	0.966
Conjunctive Rule	0.915	0.915	0.067	0.923	0.916	0.924
C4.5	0.968	0.968	0.038	0.967	0.967	0.976
NNge	0.988	0.988	0.021	0.988	0.987	0.983
OneR	0.920	0.920	0.077	0.922	0.920	0.921
Ridor	0.935	0.935	0.066	0.936	0.935	0.935
PART	0.975	0.975	0.028	0.975	0.975	0.972
DTNB	0.983	0.983	0.011	0.983	0.983	0.999

Interpretation of the Results

Various rule-based classification strategies have been  presented for detection of the CKD into two classes as ckd or notckd. The rule generated by the JRip rule learner utilizes three attributes hemo, bgr and al over the two rules for prediction as ckd and notckd. This learner achieves an accuracy of 96 % and AUC (0.959). Another rule based learner C4.5 employs six attributes and 11 rules for detecting CKD. The accuracy achieved by this learner is 96.8 % with AUC (0.976). A comparative analysis among the entire rule-based algorithms shows that DTNB i.e. Decision Table based Naïve Bayes classifier achieves lowest FP Rate (0.011) and highest area under curve (0.999). Accordingly, this study concludes that among rule-based learners DTNB is most effective in terms of ROC area.

Conclusion

In this paper, a comparative study of different rule-based classification approaches has been carried out. The performance measures of these rule-extraction methods on CKD dataset have  been depicted. The rules extracted from the different rule-based algorithms can be used as a second opinion for diagnosing CKD and identifying persons lying in higher risk groups during the progression of the disease. The study concludes that rule-based classifier DTNB i.e. DecisionTable-Naïve Bayes learner achieves the highest AUC of 99.9 % and lowest FP rate of 1.1 % . The significance of our comparative study lies with the reduced set off features through which simple and comprehensiverules are generated.The findings of this comparative analysis on rule-base learners can be used as a diagnostic tool in prediction of chronic kidney disease.

Acknowledgements and Conflict of Interest

The authors are greatly thankful to NIT Raipur for support and for providing facility, space, and an opportunity to conduct this study. The authors have no conflict of interest to declare.

References

1. Global Facts: About Kidney Disease – The National Kidney Foundation; https://www.kidney.org/kidneydisease/global-facts-about-kidney-disease.
2. CKD stages. Ren. Assoc.; http://www.renal.org/information-resources/the-uk-eckd-guide/ckd-stages#sthash.iEZ6eyX6.8cDBC6pw.dpbs.
3. Understanding Your Lab Values – The National Kidney Foundation; https://www.kidney.org/atoz/content/understanding-your-lab-values.
4. kidney-location-human-anatomy; http://cephalicvein.com/wp-content/uploads/2016/08/kidney-location-human-anatomy.jpg.
5. Kidney Function, Location &amp; Area | Body Maps; http://www.healthline.com/human-body-maps/kidney.
6. Basic Information About Kidneys | Kidney Research UK – Kidney Research UK – Kidney Research UK; https://www.kidneyresearchuk.org/health-information/resources/the-kidneys-a-basic-guide.
7. Van Balkom B. W. M., Pisitkun T., Verhaar M. C et al. Exosomes and the kidney: prospects for diagnosis and therapy of renal diseases. Kidney Int. 2011;80:1138–1145.
8. Di Noia T., Ostuni V. C., Pesce F et al. An end stage kidney disease predictor based on an artificial neural networks ensemble. Expert Syst. Appl. 2013;40:4438–4445.
9. Gunasundari S., Janakiraman S., Meenambal S. Velocity Bounded Boolean Particle Swarm Optimization for improved feature selection in liver and kidney disease diagnosis. Expert Syst. Appl. 2016;56:28–47.
10. Salekin A., Stankovic J. Detection of Chronic Kidney Disease and Selecting Important Predictive Attributes. In: In Healthcare Informatics (ICHI), IEEE International Conference. 2016;262–270.
11. Arora M., Sharma E. A. Chronic Kidney Disease Detection by Analyzing Medical Datasets in Weka. Int. J. Comput. Appl. 2016;6:20–26.
12. Rubini L. j., Eswaran P. Generating comparative analysis of early stage prediction of Chronic Kidney Disease. Int. J. Mod. Eng. Res. 2015;5:49–55.
13. Gadaras I., Mikhailov L. An interpretable fuzzy rule-based classification methodology for medical diagnosis. Artif. Intell. Med. 2009;47:25–41.
14. Krause M., Samoylenko A., Vainio S. J. Exosomes as renal inductive signals in health and disease, and their application as diagnostic markers and therapeutic agents. Front. cell Dev. Biol. 2015;3: 65.
15. Jella K. K., Yu L., Yue Q et al. Exosomal GAPDH from proximal tubule cells regulate ENaC activity. PLoS One. 2016;11:1–20.
16. Bache K., Lichman M. UCI Machine Learning Repository. 2013; http://archive.ics.uci.edu/ml
17. Hall M., Frank E., Holmes G et al. The WEKA data mining software. SIGKDD Explor. Newsl. 2009; 11:10.
18. Cohen W. W. Fast effective rule induction. In: Proceedings of the twelfth international conference on machine learning. 1995;115–123.
19. Breiman L., Friedman., Jerome H., Olshen R. et al. Classification and Regression Trees. Chapman and Hall, New York. 1984.
20. Ross J., Morgan Q., Publishers K. Book Review : C4.5 : Programs for Machine Learning. 1994;240:235–240.
21. Martin B. Instance-based Learning: Nearest Neighbour with Generalisation. 1995.
22. Holte R.C. Very Simple Classi fi cation Rules Perform Well on Most Commonly Used Datasets. Mach. Learn. 1993;11:63–91.
23. Gaines B. R., Compton P. Induction of ripple-down rules applied to modeling large databases. J. Intell. Inf. Syst. 1995;5:211–228.
24. Frank E., Witten I. H. Generating accurate rule sets without global optimization. Proc. Fifteenth Int. Conf. Mach. Learn. 1998;144–151.
25. Hall M, Frank E. Combining Naive Bayes and Decision Tables. In: In FLAIRS Conference. 2008;318–319.